Data compression
I have been curious about how data compression works for a very long time - back in the day there was an archiver race, with WinRar and KGB archiver being insanely good at it. Bear in mind, those were the days where you had to use 1.44MB 3.5" magnetic "floppy" disks to transfer data - that was the era before DVD and even CD disks. And what WinRar could offer was no joke - you could compress 14MB Doom 2 and split it into 5 tomes, write each of them to a separate disk and then unarchive them on another computer - archiver would prompt you to insert the next disk with the next tome when it is done decompressing the current one.
But I digress. I was curious how WinRar can do that and how the size of the data is actually reduced.
And recently I got back to this topic. What I found was actually quite interesting.
Back in the day I had an idea to transform the data like so: for each character, replace it with a short code followed by the number of times it is repeated in a row:
AAAAABBB (8 characters)
|
v
A5B3 (4 characters - 50% compression!)
This is exactly what run-length encoding is doing. The problem with this solution was that even this very text does not contain a whole lot of repeated characters in a row, so it is quite inefficient:
Hello world (11 characters)
|
v
H1e1l2o1 1w1o1r1l1d1 (20 characters - negative 100% compression)
The next idea I had was to represent each character's original binary code with a shorter one:
Hello world
H (72 = 01001000 => 000000001)
e (101 = 01100101 => 00000010)
l (108 = 01101100 => 00000011) <------\
l (108 = 01101100 => 00000011) <-----/|
o (111 = 01101111 => 00000100) <-\ |
(32 = 00100000 => 00000101) | |
w (119 = 01110111 => 00000110) | |
o (111 = 01101111 => 00000100) <-/ |
r (114 = 01110010 => 00000111) |
l (108 = 01101100 => 00000011) <------/
d (100 = 01100100 => 00001000)
Original:
Hello world
01001000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100
New:
00000001 00000010 00000011 00000011 00000100 00000101 00000110 00000100 00000111 00000011 00001000
On itself this does not present any compression, but what if characters were packed into half-bytes? The longest short code is only 4 (meaningful) bits, so we could get rid of most of zeros:
Old:
0000'0001 0000'0010 0000'0011 0000'0011 0000'0100 0000'0101 0000'0110 0000'0100 0000'0111 0000'0011 0000'1000
(11 bytes)
New:
0001'0010 0011'0011 0100'0101 0110'0100 0111'0011 1000'0000
(6 bytes)
This is a reduction of about 50%! But this method does not preserve the mapping of characters to short codes. If we were to add this mapping, the message size would be actually much larger:
01001000 00000001 01100101 00000010 01101100 00000011 01101111 00000100 00100000 00000101 01110111 00000110 01110010 00000111 01100100 00001000
H code e code l code o code <space> code w code r code d code
This is already 16 bytes. Then add the 6 bytes for the encoded message and you get 22 bytes - a -100% (negative 100%) compression again.
If the initial text was much, much longer, this could actually be an improvement, but here's the challenge: once the number of unique letters in the initial text is larger than 15 (the maximum number of variants that could be represented by 4 bits), the compression rate drops below zero - simply because we can not represent every character in less than a full byte anymore.
Literal decades of break and I learned about Huffman encoding. The idea is somewhat similar - represent each letter of the input text with a short(er) code. The algorithm looks like this: get all the unique letters of the input text, order them by the number of their occurrences in the text, in decreasing order:
l => 3
o => 2
d => 1
r => 1
w => 1
" " => 1
e => 1
H => 1
Within this list, order the pairs with the same number of occurrences by the character code, in ascending order:
l => 3
o => 2
" " => 1
H => 1
d => 1
e => 1
r => 1
w => 1
Imagine each of these entries as a node:

Then, take a pair of nodes with the smallest number of occurrences each and merge them into a new node with the number of occurrences as a sum of two original nodes:
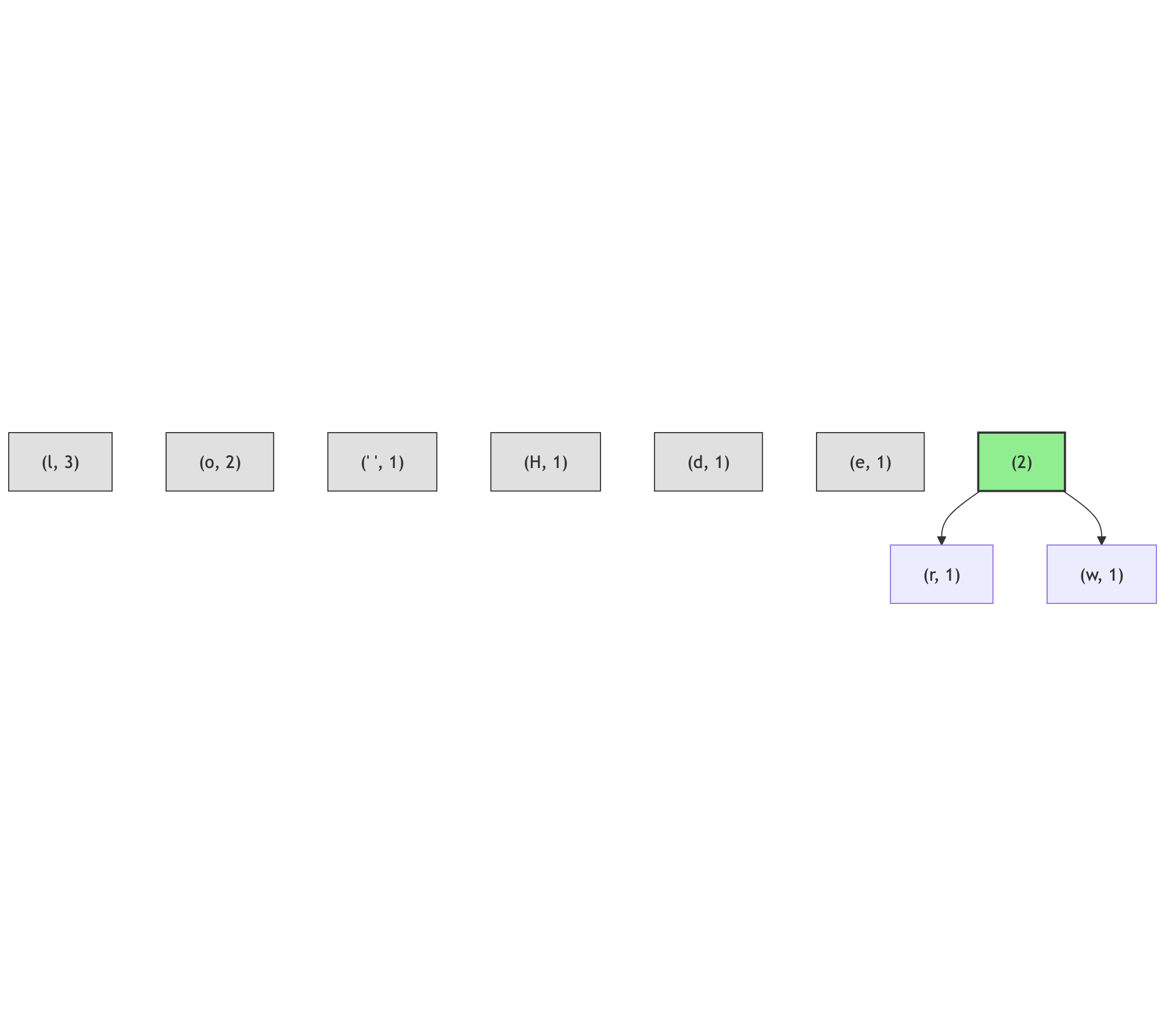
Repeat this process until there is just one node left:
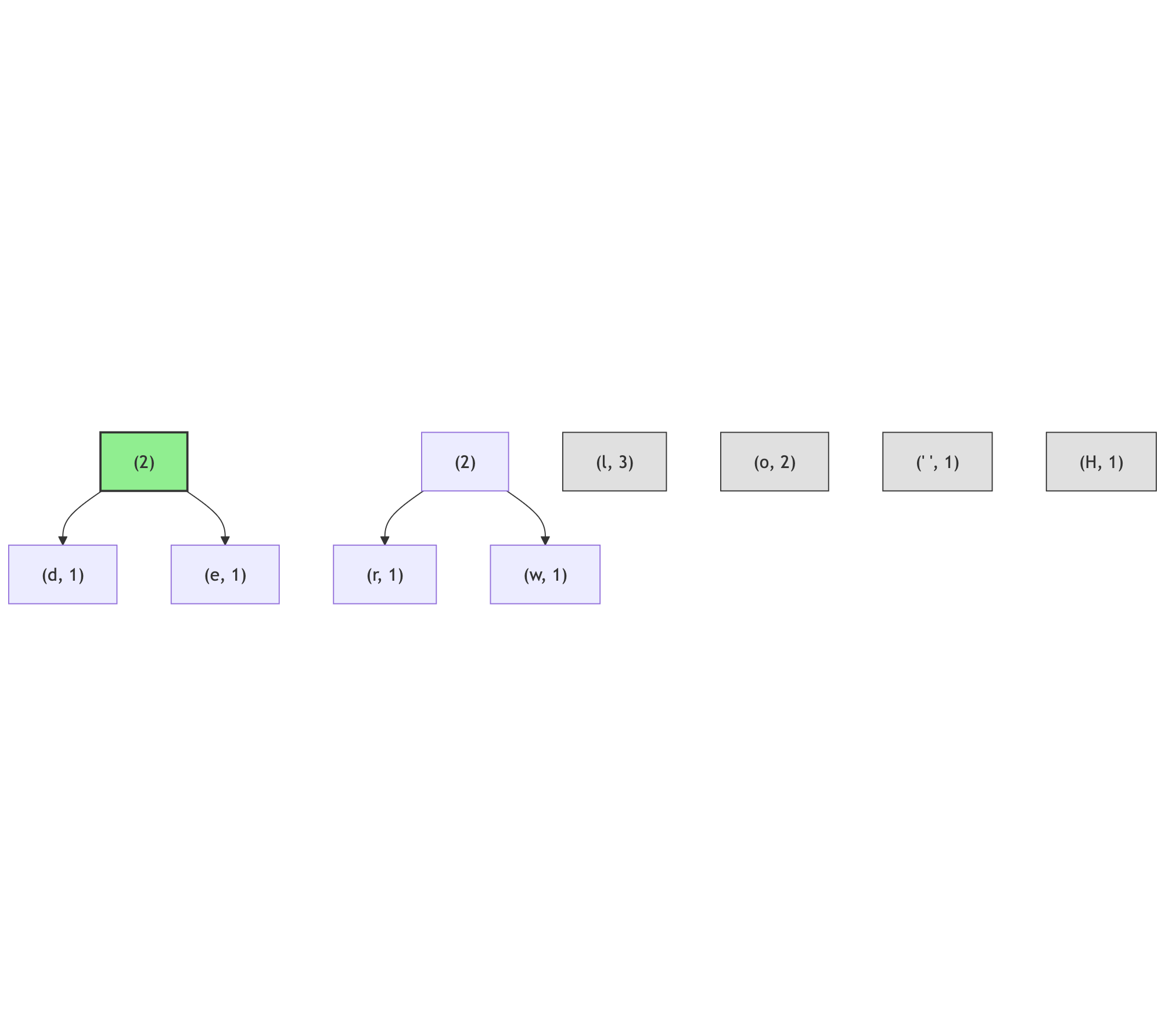
And again:
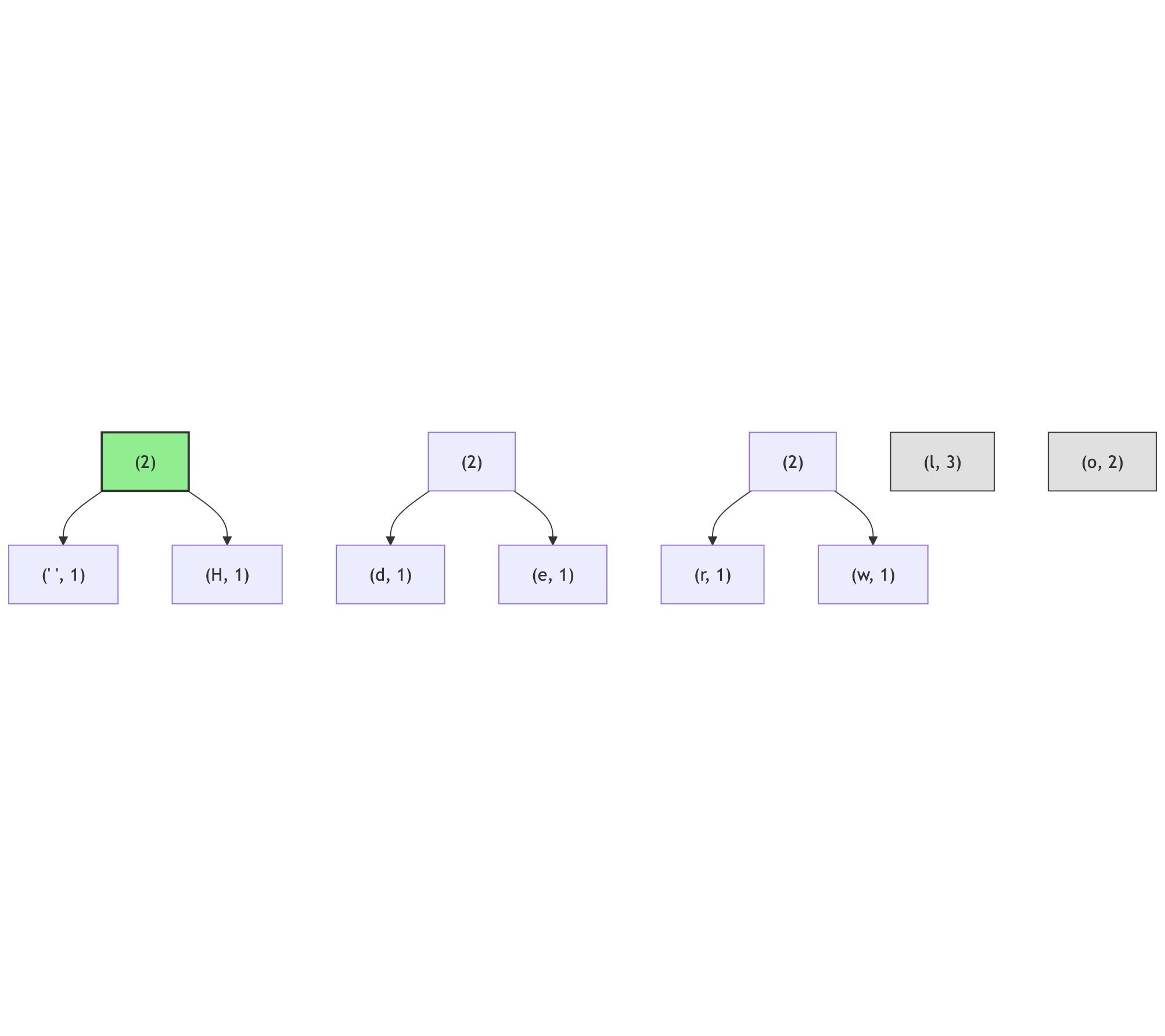
There are four candidates for the smallest amongst the (2) nodes: (o, 2) and three internal nodes; in this case the (o, 2) node will become the left branch (because the ordering of the characters - none of the internal nodes has the character assigned, but the (o, 2) node has it; its code is lexicographically larger than the empty character, assuming empty character has code of 0):
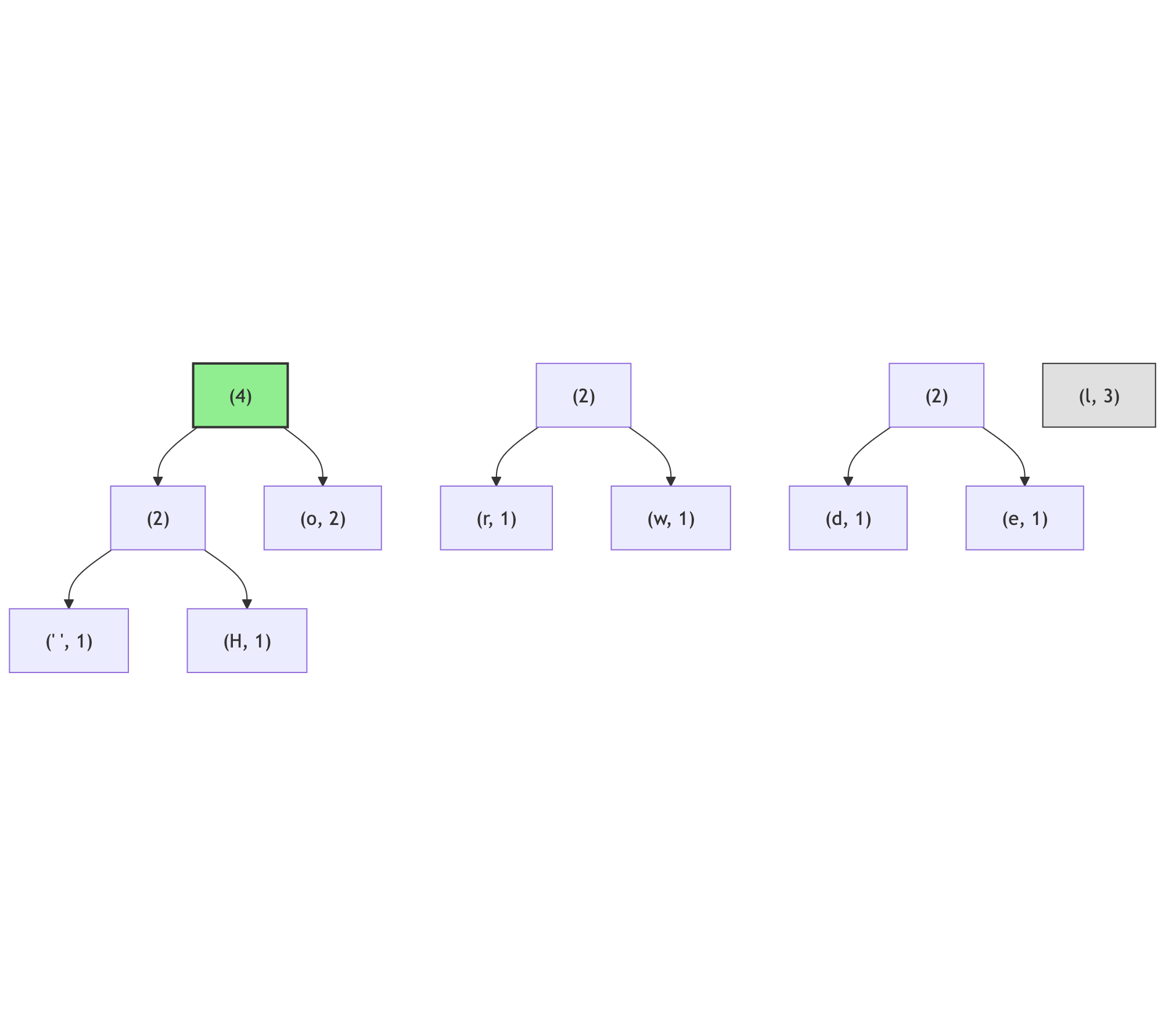
Note how the node (l, 3) has moved to the middle of the list, between (4) and (2) nodes - this is needed to preserve the ordering by the number of occurrences.
There are two more nodes (2), join them:
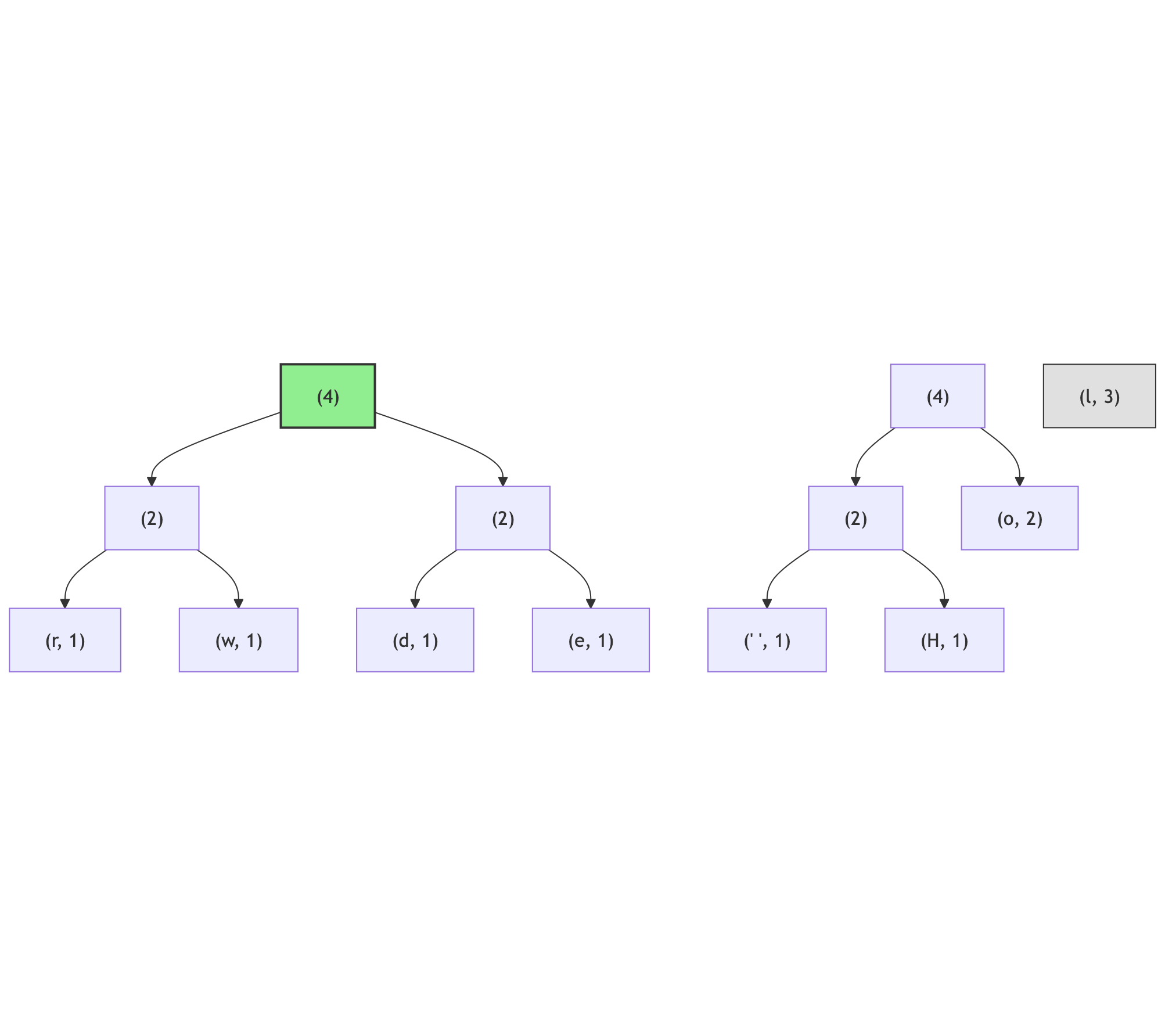
Now the smallest two nodes are (l, 3) and (4):
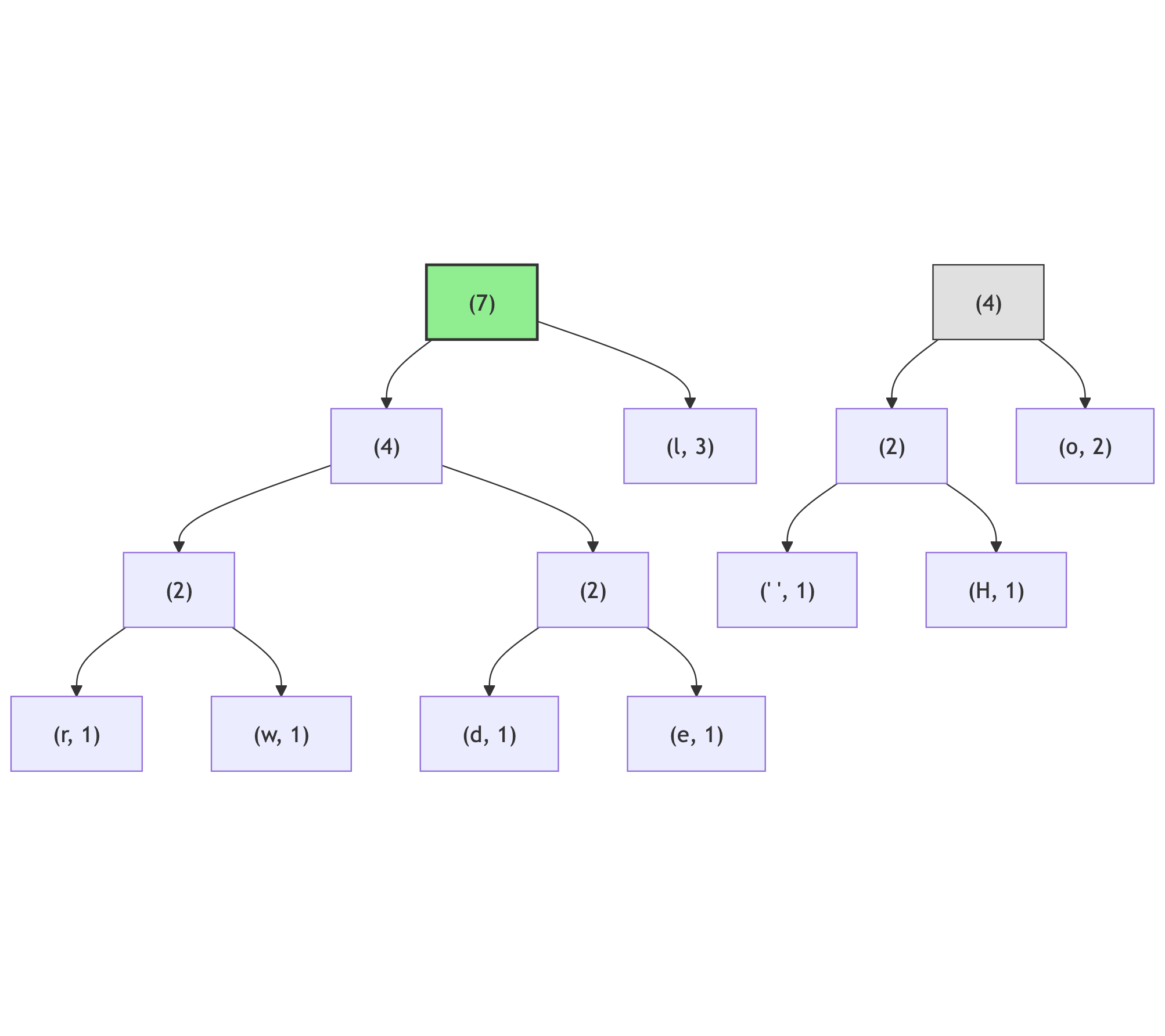
And lastly there are (7) and (4) nodes to merge:
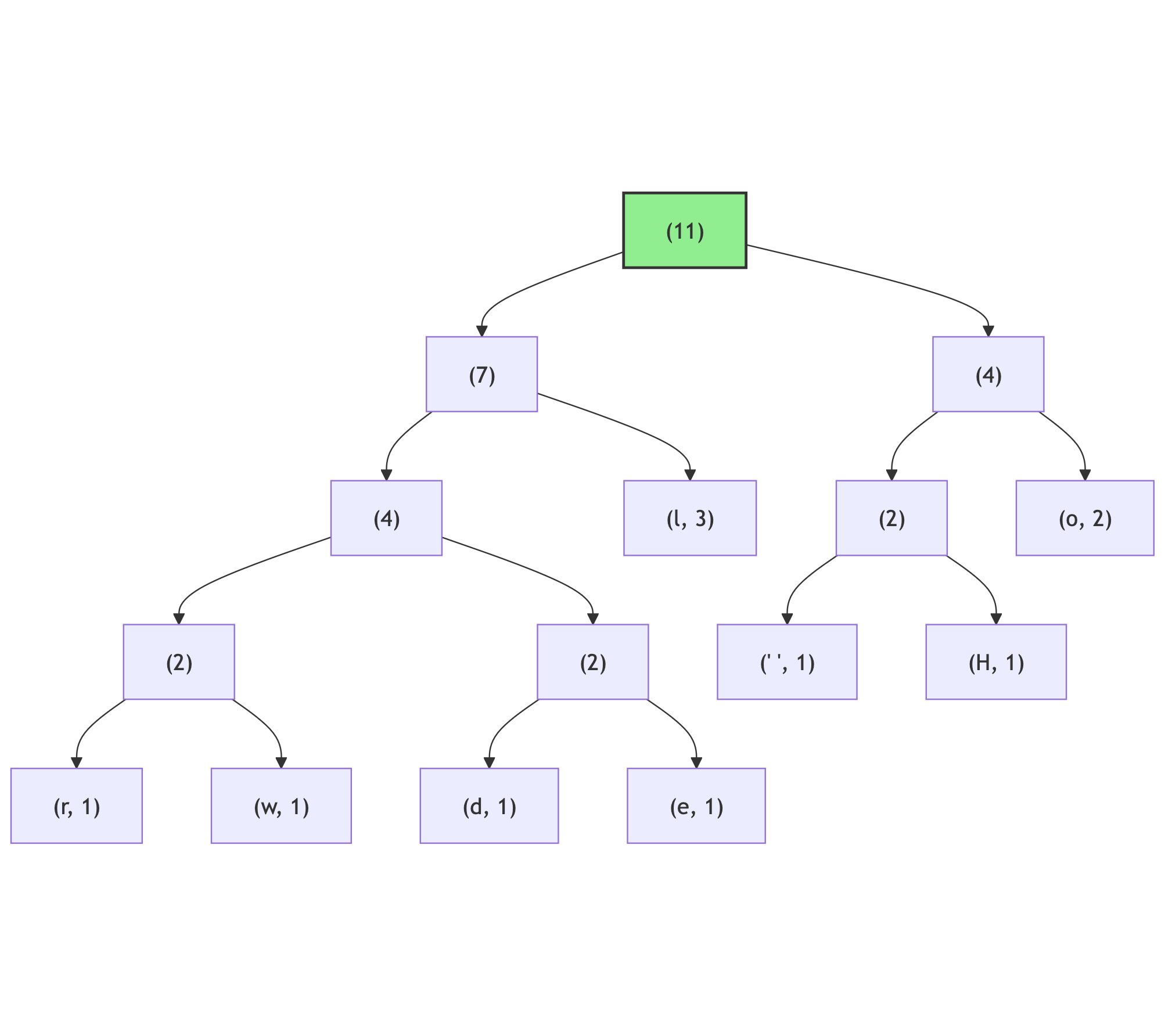
Then, following the rule "left branch -> '0', right branch -> '1'", mark each branches of this tree:
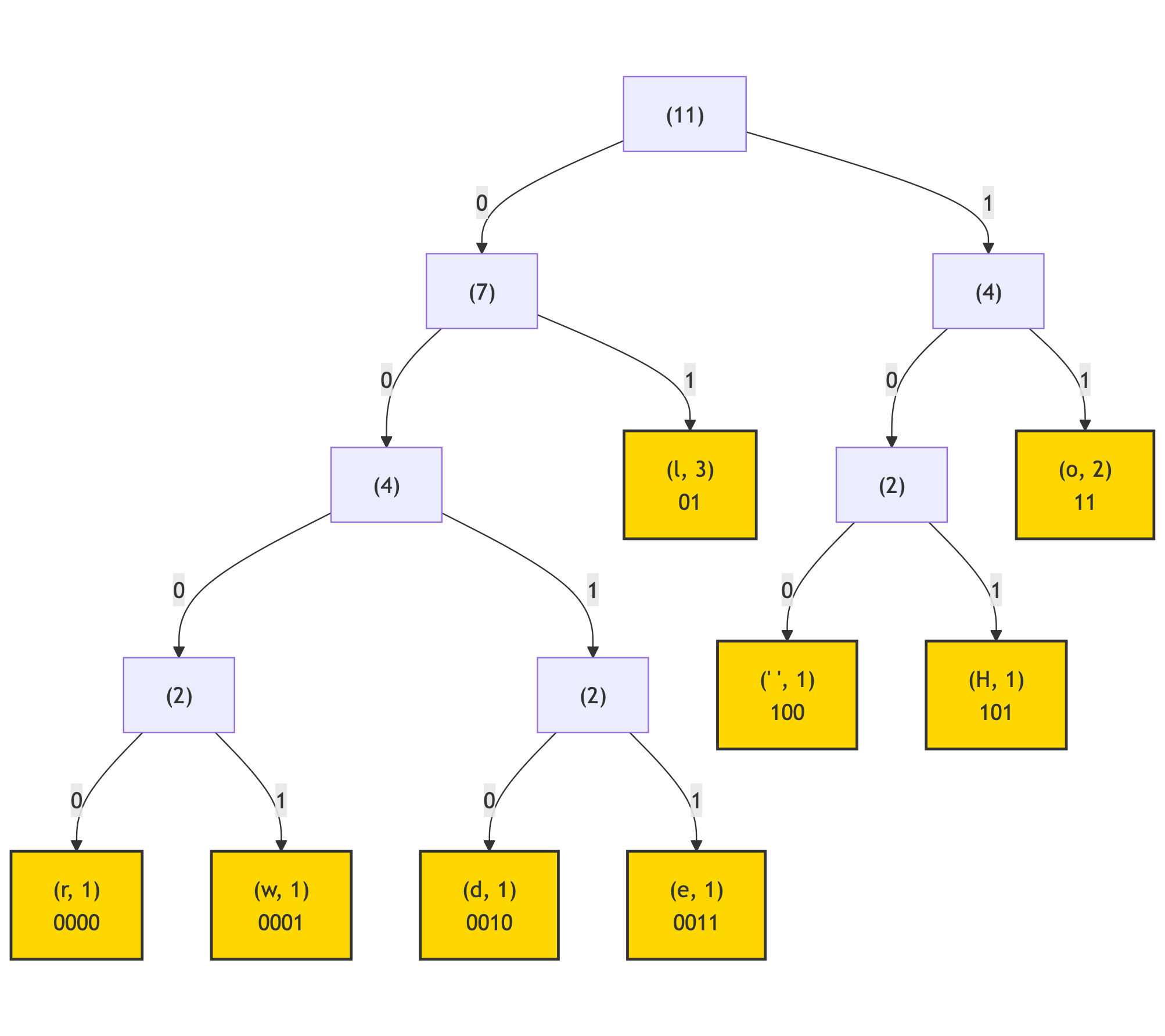
Lastly, by following the branches from the root node of this tree, gather the branch labels into the binary code for each of the leaf nodes:
(l, 3, 0b01) (o, 2, 0b11) (" ", 1, 0b100) (H, 1, 0b101) (d, 1, 0b0010) (e, 1, 0b0011) (r, 1, 0b0000) (w, 1, 0b0001)
This is called Huffman encoding or Huffman tree.
Using these codes, the initial text Hello world is encoded as following:
H e l l o w o r l d
101 0011 01 01 11 100 0001 11 0000 01 0010
joining into bytes
10100110 10111100 00011100 00010010
This could be programmed in Ruby like so:
s = 'Hello world'
a = s.chars.uniq.map {|c| {char: c, count: s.chars.count(c)}}.sort {|a, b| [b[:count], a[:char]] <=> [a[:count], b[:char]]}
pq = a.map { |c| {char: c[:char], count: c[:count], left: nil, right: nil} }
while pq.size > 1 do
left, right = pq.pop(2)
if left[:count] < right[:count]
left, right = right, left
end
pq << {char: nil, count: left[:count] + right[:count], left: left, right: right}
pq.sort! {|a,b| [b[:count], a[:char] || ''] <=> [a[:count], b[:char] || '']}
end
q = [{node: pq[0], code: ''}]
codes = {}
while q.size > 0 do
e = q.shift
if e[:node][:left].nil? && e[:node][:right].nil?
codes[e[:node][:char]] = e[:code]
next
end
q.push({node: e[:node][:left], code: e[:code] + '0'}) if !e[:node][:left].nil?
q.push({node: e[:node][:right], code: e[:code] + '1'}) if !e[:node][:right].nil?
endor in C++:
#include <string>
#include <map>
#include <queue>
#include <iostream>
struct Node {
char c;
int count;
Node* left;
Node* right;
};
struct CodeNode {
Node* node;
std::string code;
};
int main() {
const std::string s = "Hello world";
std::map<char, int> freq;
for (auto i : s) {
if (freq.find(i) == freq.end()) {
freq[i] = 1;
} else {
freq[i]++;
}
}
auto cmpNode = [](Node* a, Node* b) {
if (a->count != b->count) {
return a->count > b->count;
}
if ((a->c == static_cast<char>(255)) != (b->c == static_cast<char>(255))) {
return b->c == static_cast<char>(255);
}
return a->c < b->c;
};
std::priority_queue<Node*, std::vector<Node*>, decltype(cmpNode)> pq(cmpNode);
for (auto i : freq) {
pq.push(new Node{.c = i.first, .count = i.second, .left = nullptr, .right = nullptr});
}
while (pq.size() > 1) {
auto* left = pq.top();
pq.pop();
auto* right = pq.top();
pq.pop();
if (left->count < right->count) {
std::swap(left, right);
}
pq.push(new Node{ .c = static_cast<char>(255), .count = left->count + right->count, .left = left, .right = right });
}
std::queue<CodeNode*> q;
q.push(new CodeNode{ .node = pq.top(), .code = std::string() });
std::map<char, std::string> codes;
while (!q.empty()) {
auto* e = q.front();
q.pop();
if (!e->node->left && !e->node->right) {
codes[e->node->c] = e->code;
continue;
}
if (e->node->left) {
q.push(new CodeNode{ .node = e->node->left, .code = e->code + "0" });
}
if (e->node->right) {
q.push(new CodeNode{ .node = e->node->right, .code = e->code + "1" });
}
}
for (auto i : codes) {
std::cout << "'" << i.first << "'" << ": " << i.second << std::endl;
}
return 0;
}If the Huffman table is known, the source could be decoded by traversing from the root: if the next bit in the input sequence is 0 - traverse the left child of the current node, if the next bit is 1 - traverse the right child of the current node; if the leaf node is reached - emit a corresponding character:
In Ruby:
encoded = s.chars.map {|c| codes[c]}.join
tree = pq[0]
def decode(tree, encoded)
root = tree
res = ''
encoded.chars.each do |c|
root = if c == '0' then root[:left] else root[:right] end
if not root[:char].nil?
res += root[:char]
root = tree
end
end
res
endOr in C++:
#include <string>
#include <map>
#include <queue>
#include <iostream>
struct Node {
char c;
int count;
Node* left;
Node* right;
};
struct CodeNode {
Node* node;
std::string code;
};
Node* buildHuffmanTree(std::string_view s) {
std::map<char, int> freq;
for (auto i : s) {
if (freq.find(i) == freq.end()) {
freq[i] = 1;
} else {
freq[i]++;
}
}
auto cmpNode = [](Node *a, Node *b) {
if (a->count != b->count) {
return a->count > b->count;
}
if ((a->c == static_cast<char>(255)) != (b->c == static_cast<char>(255))) {
return b->c == static_cast<char>(255);
}
return a->c < b->c;
};
std::priority_queue<Node *, std::vector<Node *>, decltype(cmpNode)> pq(
cmpNode);
for (auto i : freq) {
pq.push(new Node{
.c = i.first, .count = i.second, .left = nullptr, .right = nullptr});
}
while (pq.size() > 1) {
auto *left = pq.top();
pq.pop();
auto *right = pq.top();
pq.pop();
if (left->count < right->count) {
std::swap(left, right);
}
pq.push(new Node{.c = static_cast<char>(255),
.count = left->count + right->count,
.left = left,
.right = right});
}
return pq.top();
}
std::string encode(Node* tree, std::string_view s) {
std::queue<CodeNode *> q;
q.push(new CodeNode{.node = tree, .code = std::string()});
std::map<char, std::string> codes;
while (!q.empty()) {
auto *e = q.front();
q.pop();
if (!e->node->left && !e->node->right) {
codes[e->node->c] = e->code;
continue;
}
if (e->node->left) {
q.push(new CodeNode{.node = e->node->left, .code = e->code + "0"});
}
if (e->node->right) {
q.push(new CodeNode{.node = e->node->right, .code = e->code + "1"});
}
}
std::string res = "";
for (auto ch : s) {
res += codes[ch];
}
return res;
}
std::string decode(Node* tree, std::string_view s) {
std::string res = "";
auto root = tree;
for (auto ch : s) {
if (ch == '0') {
root = root->left;
} else {
root = root->right;
}
if (!root->left && !root->right) {
res += root->c;
root = tree;
}
}
return res;
}
int main() {
const std::string s = "Hello world";
auto root = buildHuffmanTree(s);
auto encoded = encode(root, s);
auto decoded = decode(root, encoded);
std::cout << "Input: " << s << std::endl;
std::cout << "Encoded: " << encoded << std::endl;
std::cout << "Decoded: " << decoded << std::endl;
return 0;
}To construct a Huffman tree from encodings table (given the encodings are sorted in the descending order of their frequency), a very simple algorithm is used - traverse the tree by the bits of the character encoding and if there is no node matched, add to the last seen node - a left child if a bit is 0 or a right child if a bit is 1.
As an example from above, consider the following encodings table (sorted already):
l => 0b01; o => 0b11; " " => 0b100; H => 0b101; d => 0b0010; e => 0b0011; r => 0b0000; w => 0b0001
Iterate over the encodings one by one, starting with l => 0b01:
encoding: (l, 0b01)
tree is empty (has only root node), the current node is root:
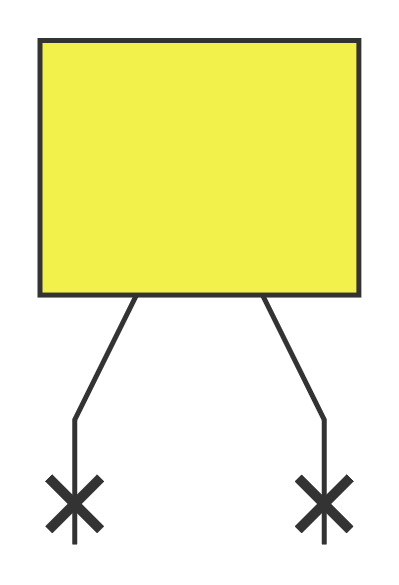
first bit: 0, add a new left child to the current node and make this new child node the current one:
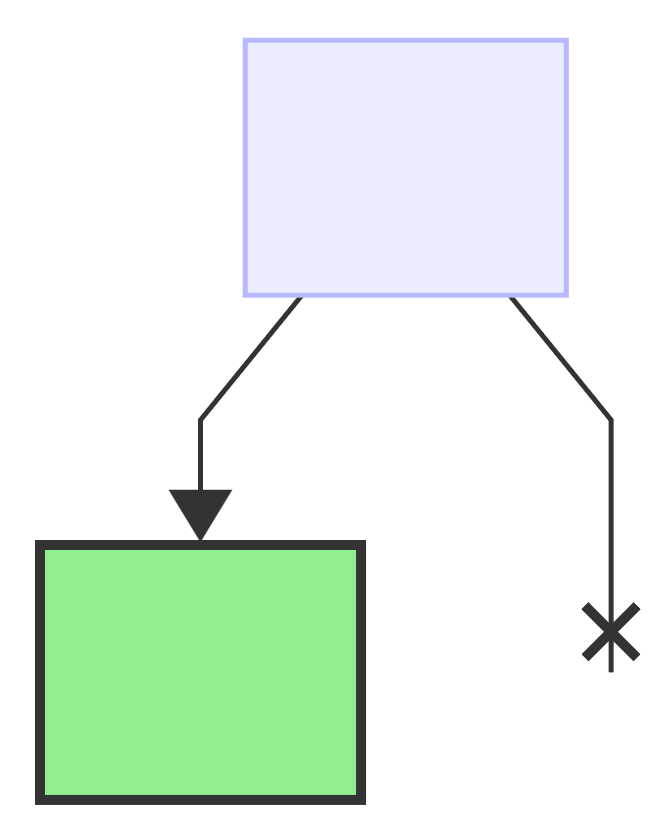
next bit: 1, add a new right child to the previously added node and make it the new current node:
since this is the last bit, add the value to the current node:
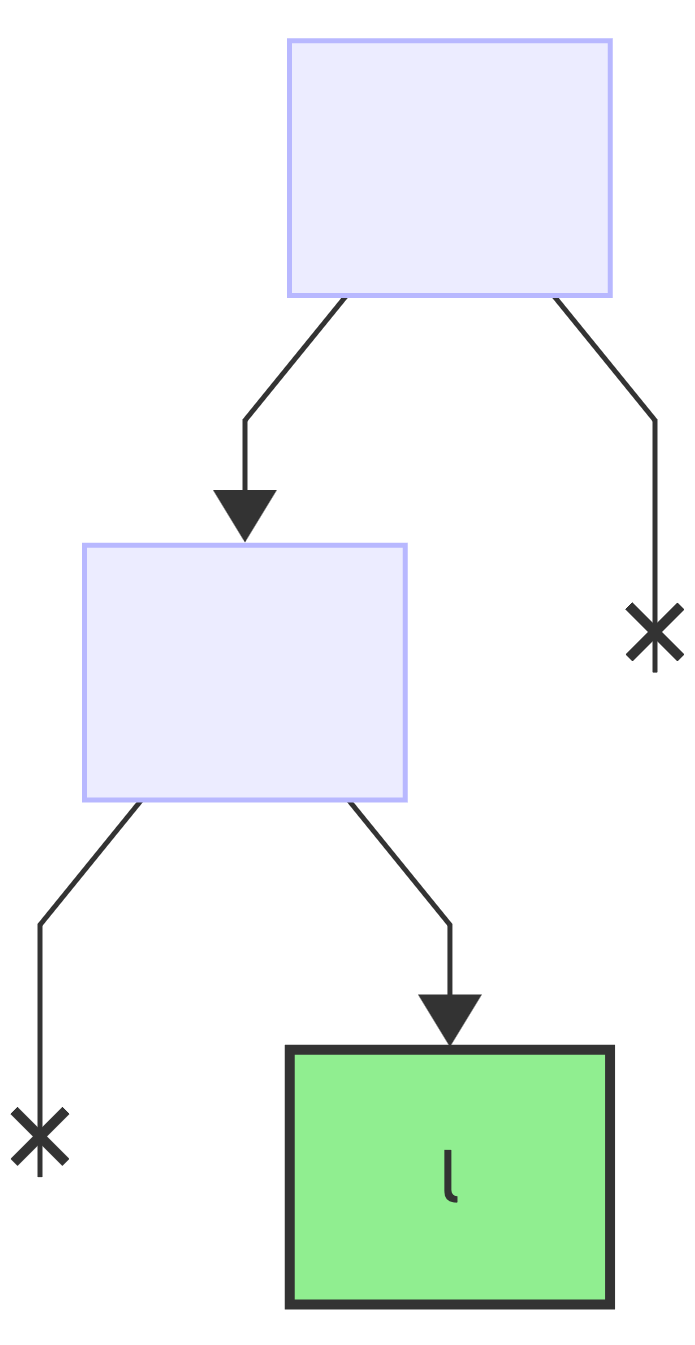
Next encoding, o => 0b11, reset the current node to the root:
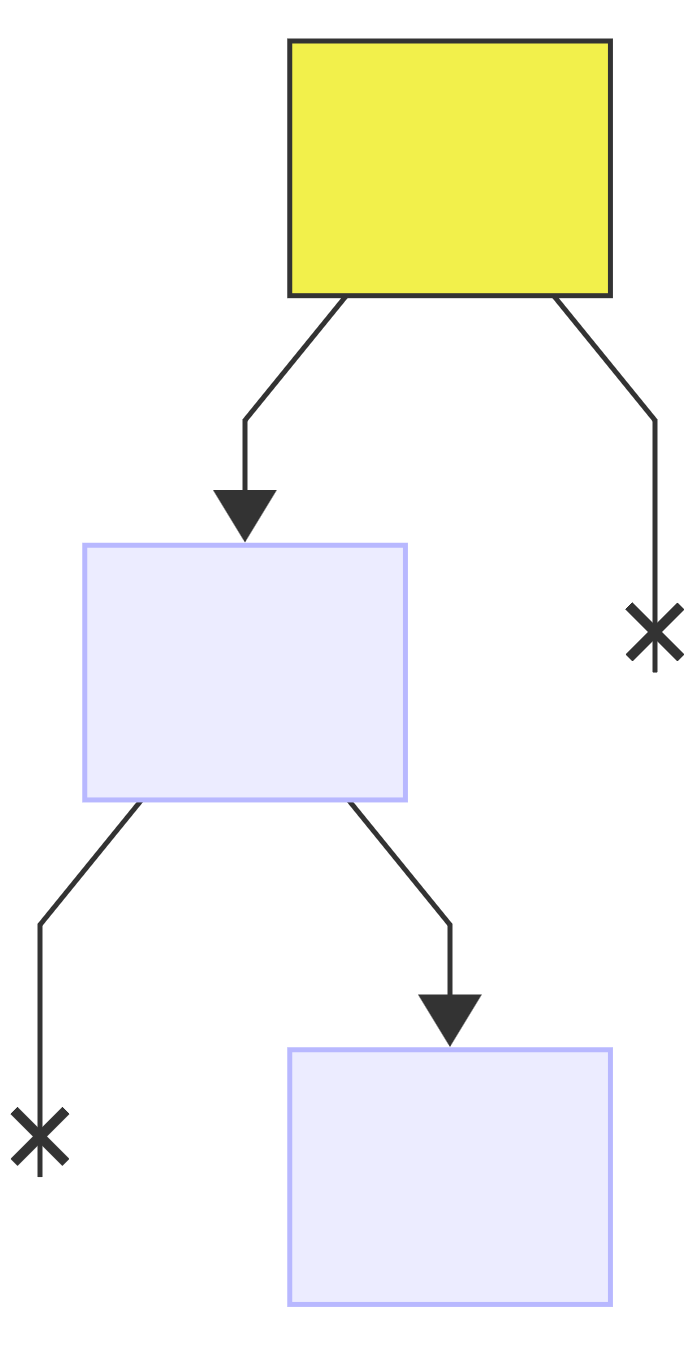
first bit: 1, add a new right child node to the current node and make it the new current:
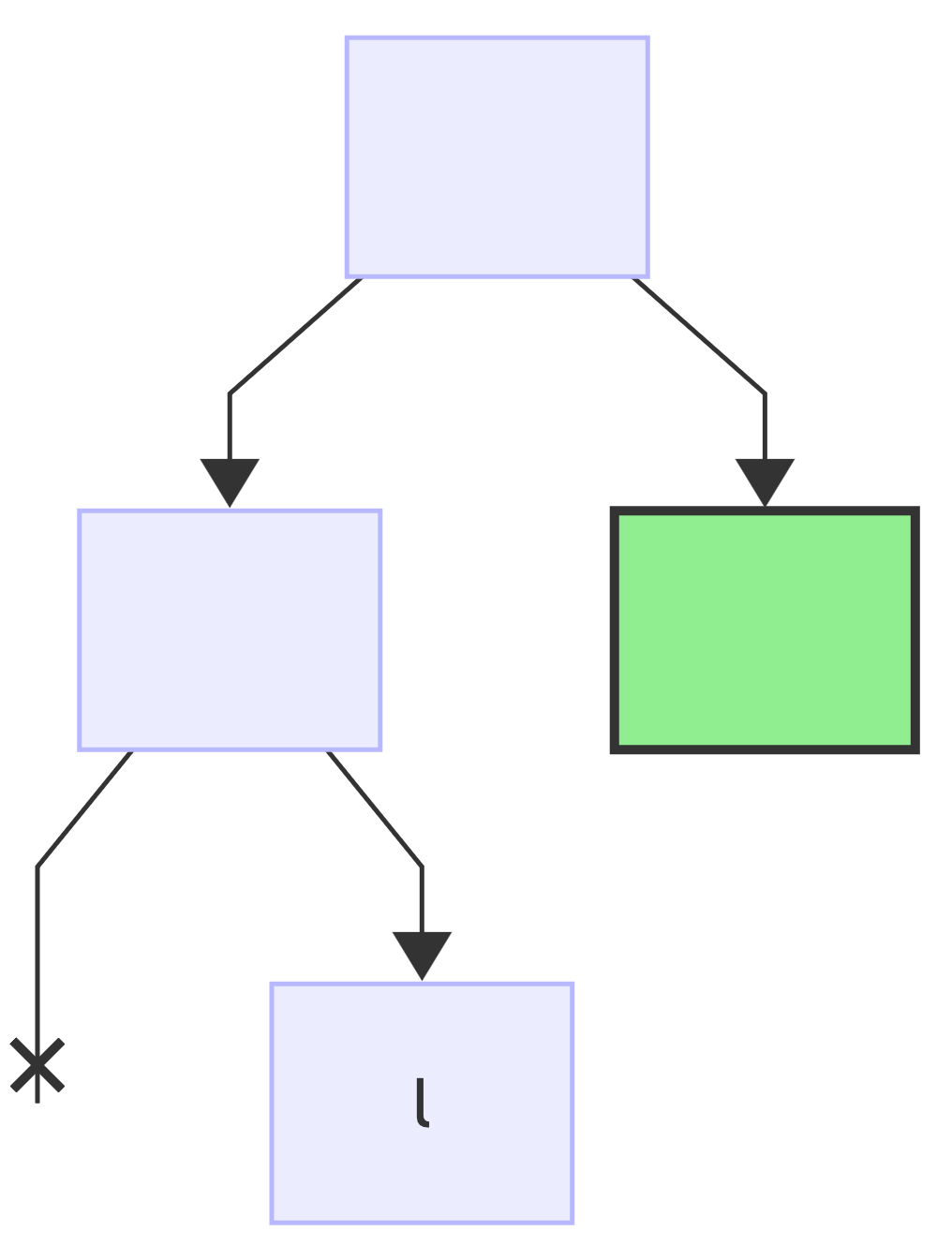
next bit: 1, add a new right child node and make it current:
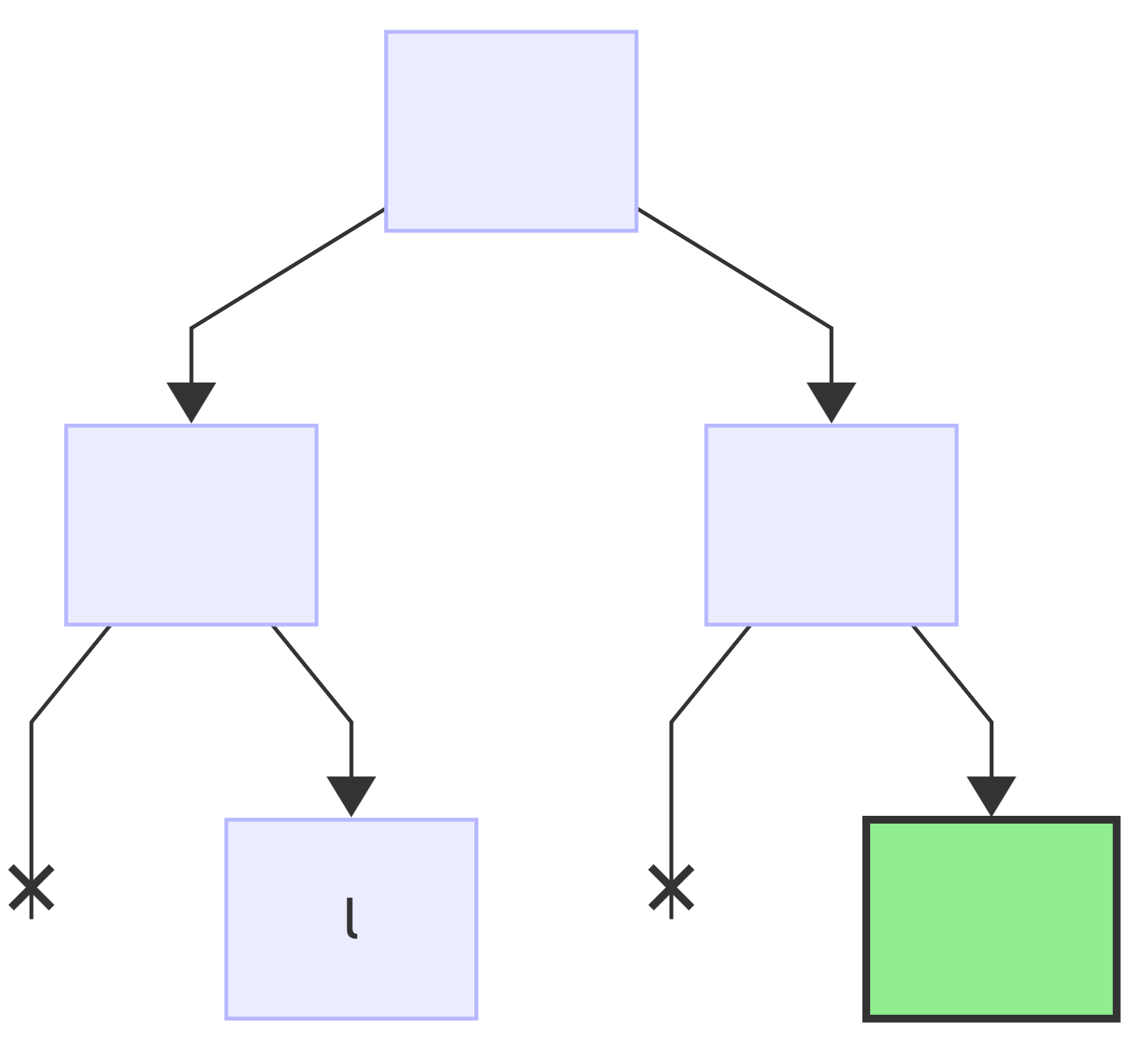
since this is the last bit, add the value to the current node:
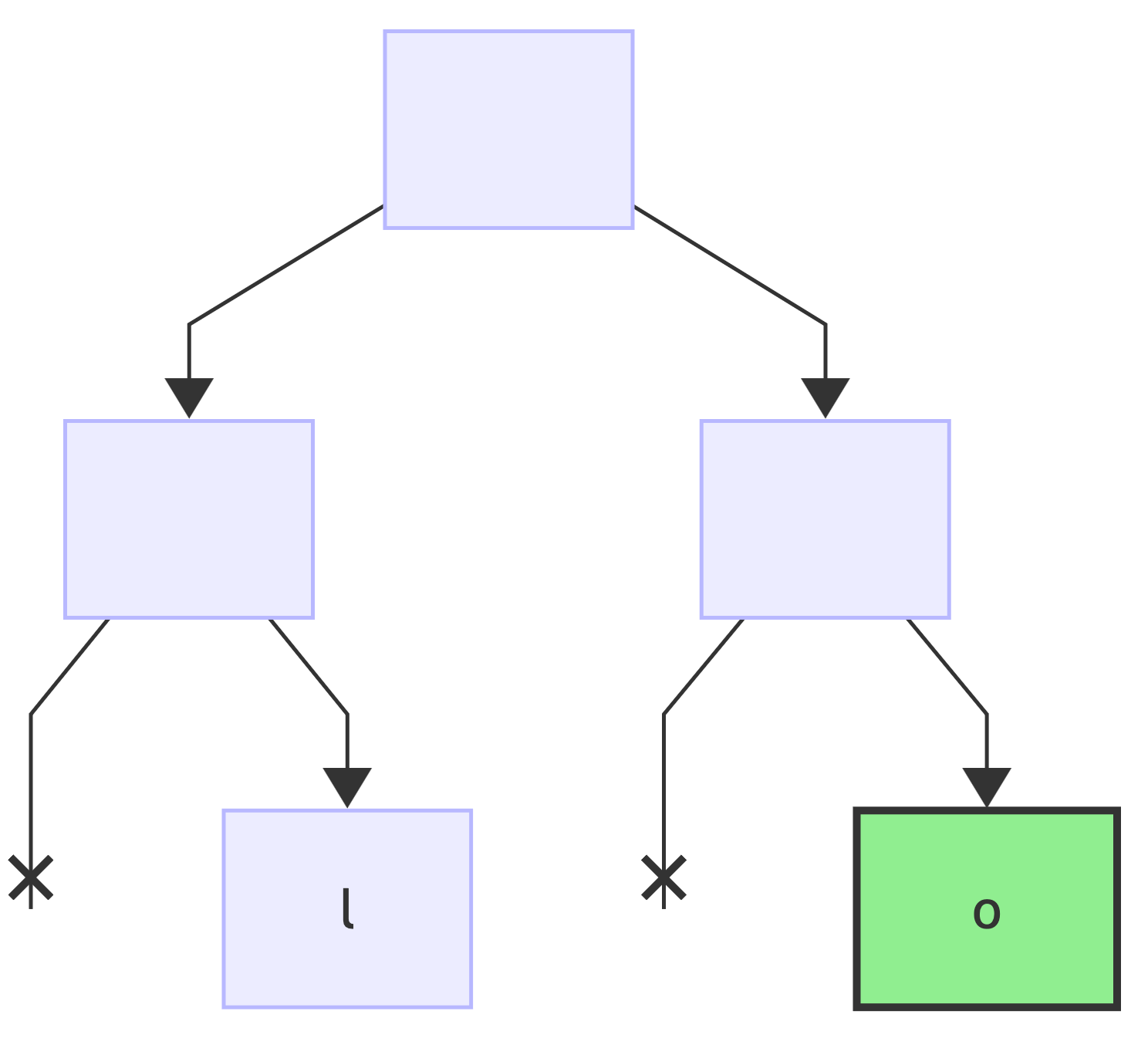
Next encoding, " " => 0b100, reset the current node (*) to the root:
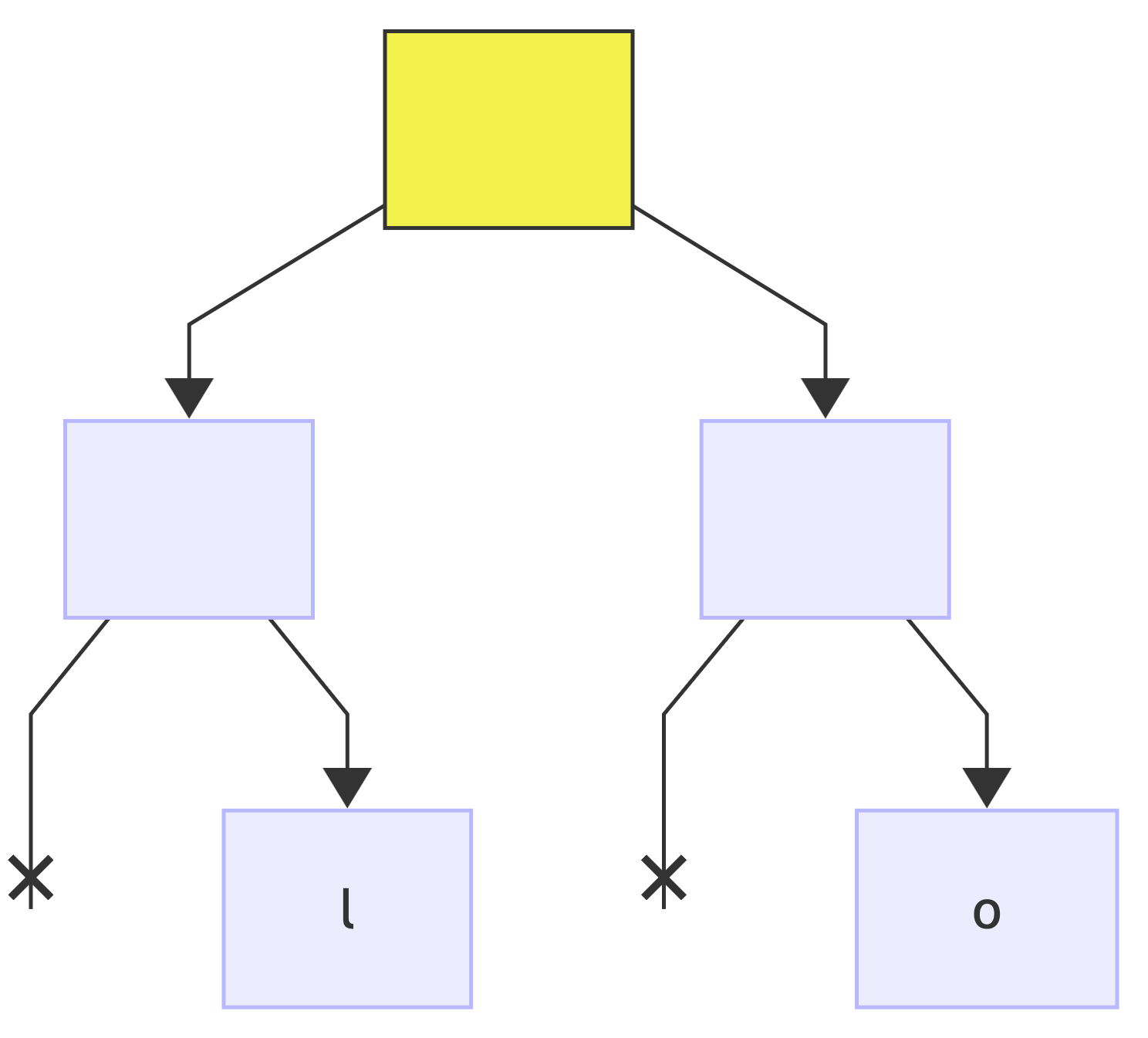
first bit: 1, no changes to the tree, since the right child of the current node exists:
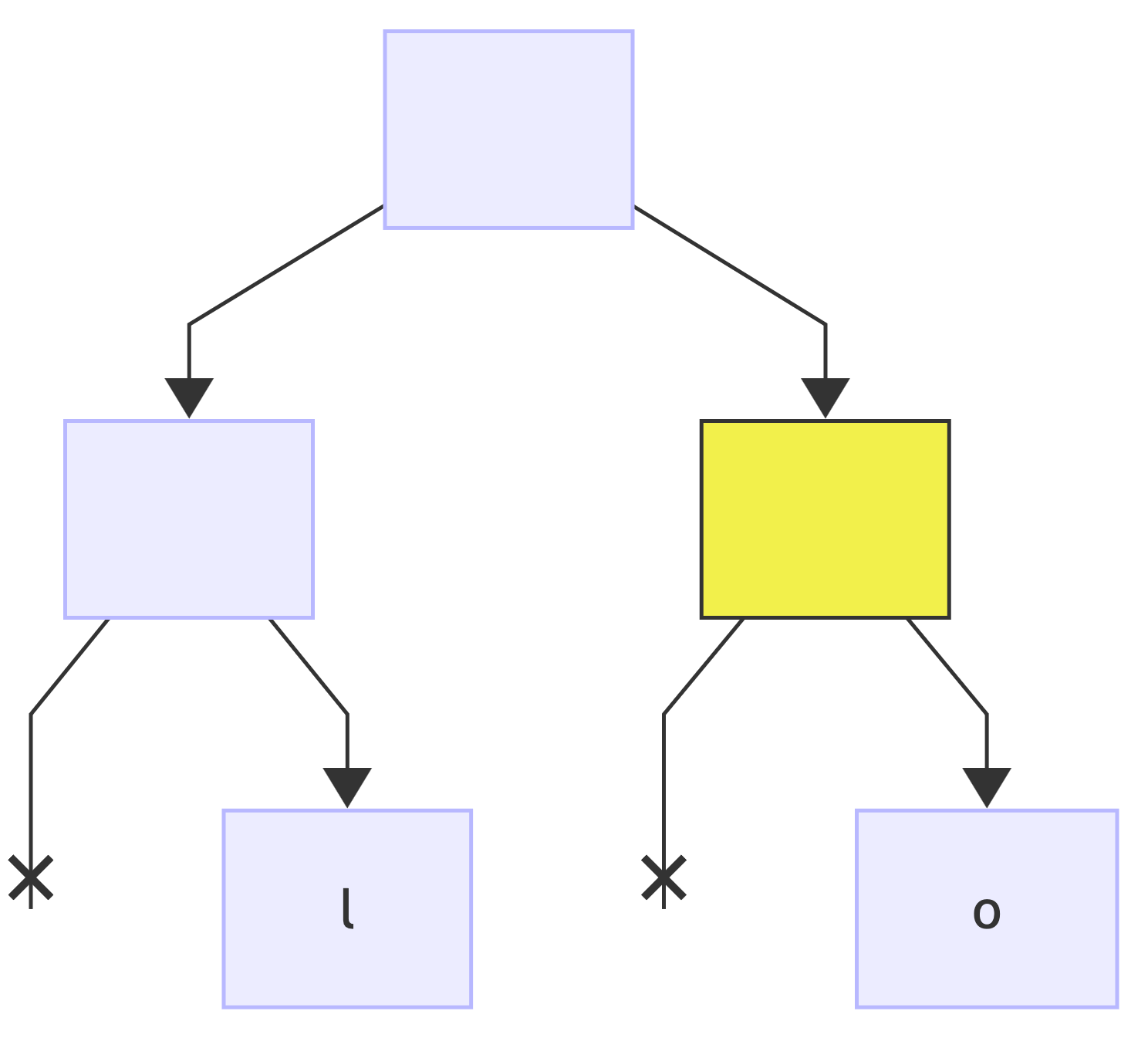
next bit: 0, add a new left child to the current node and make it the new current (*):
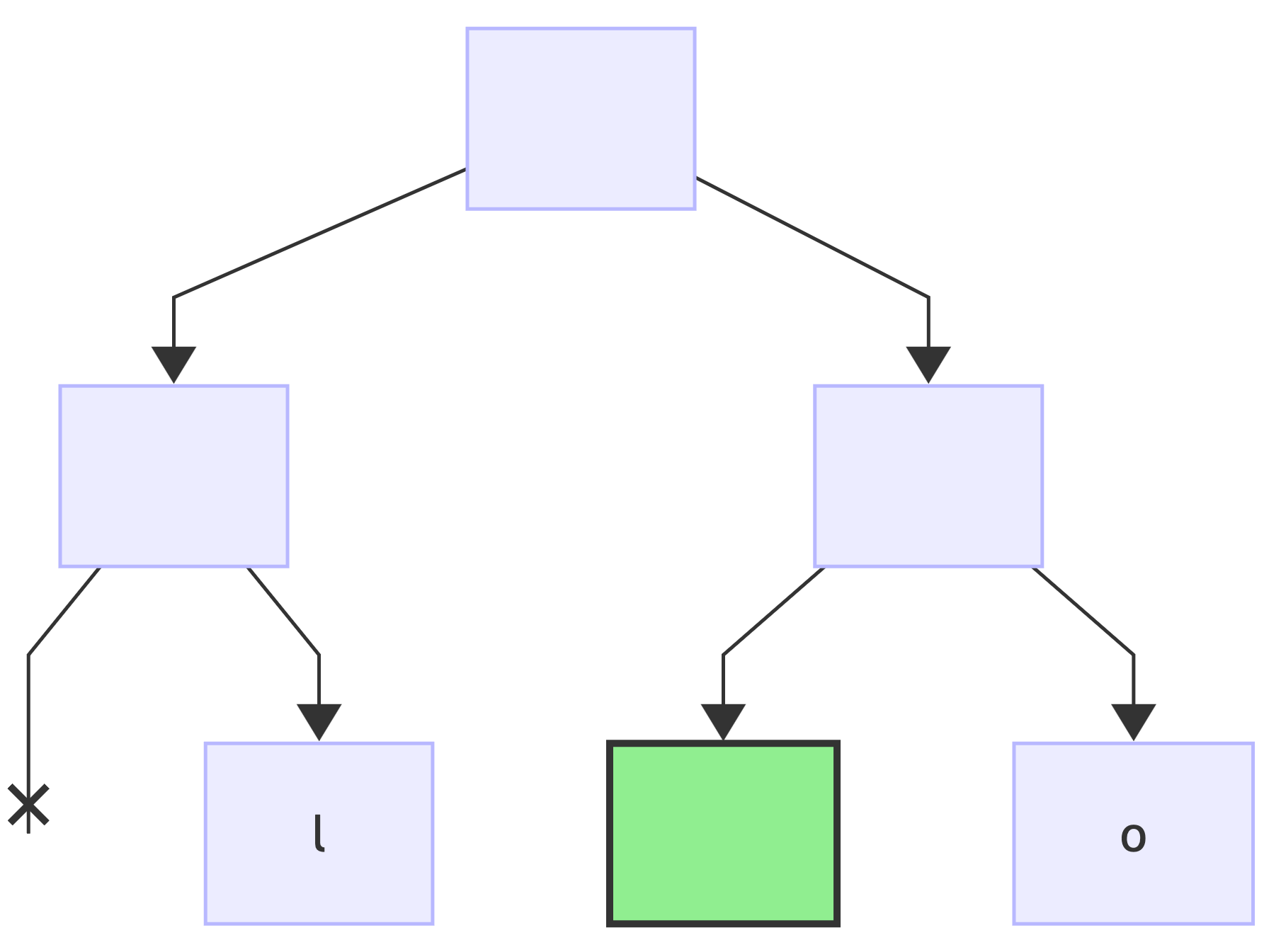
next bit: 0, add a new left child to the current node and make it the new current (*):
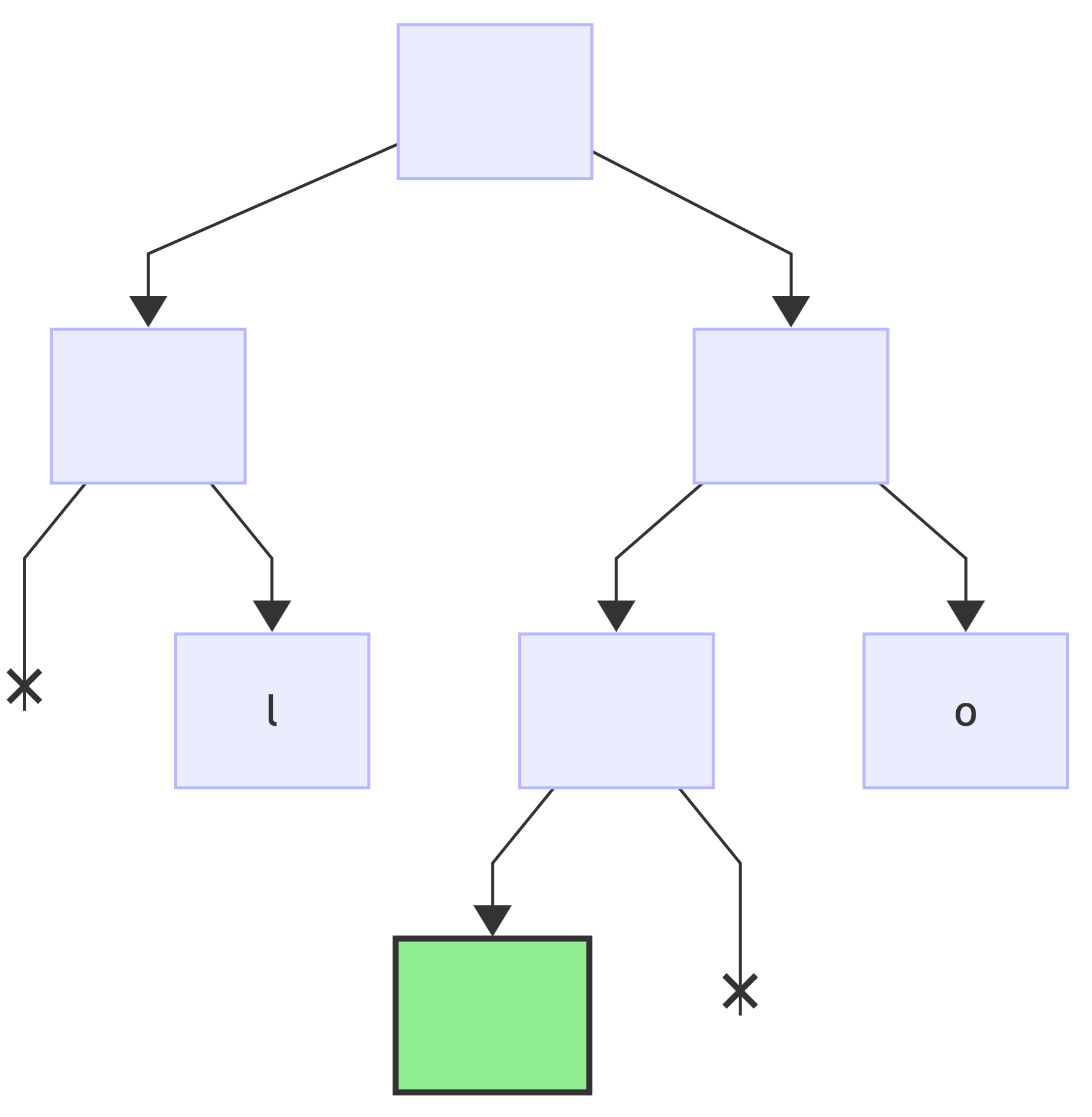
since this is the last bit, add a value to the current node:
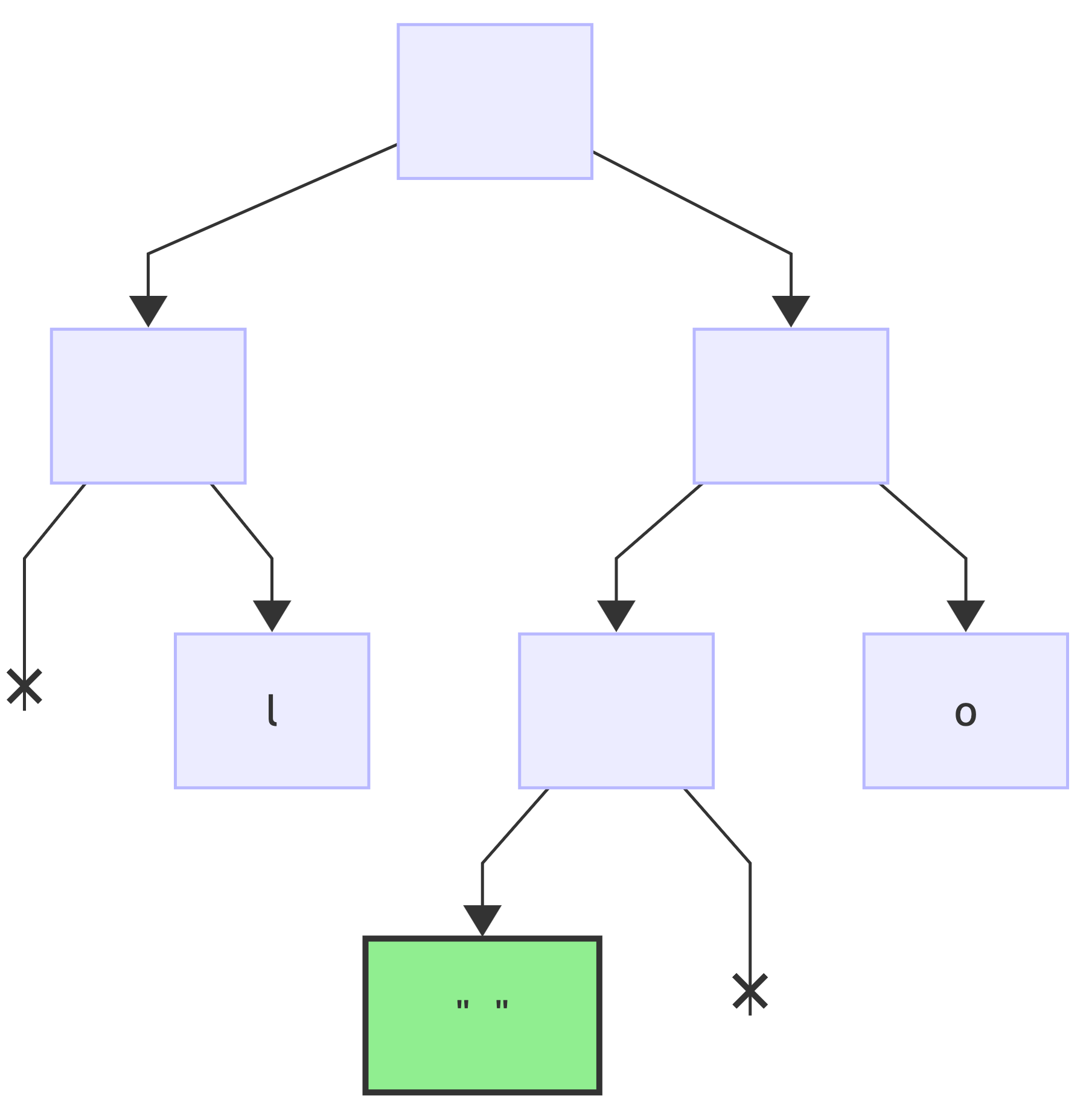
Next encoding is H => 0b101, reset the current node (*) to root:
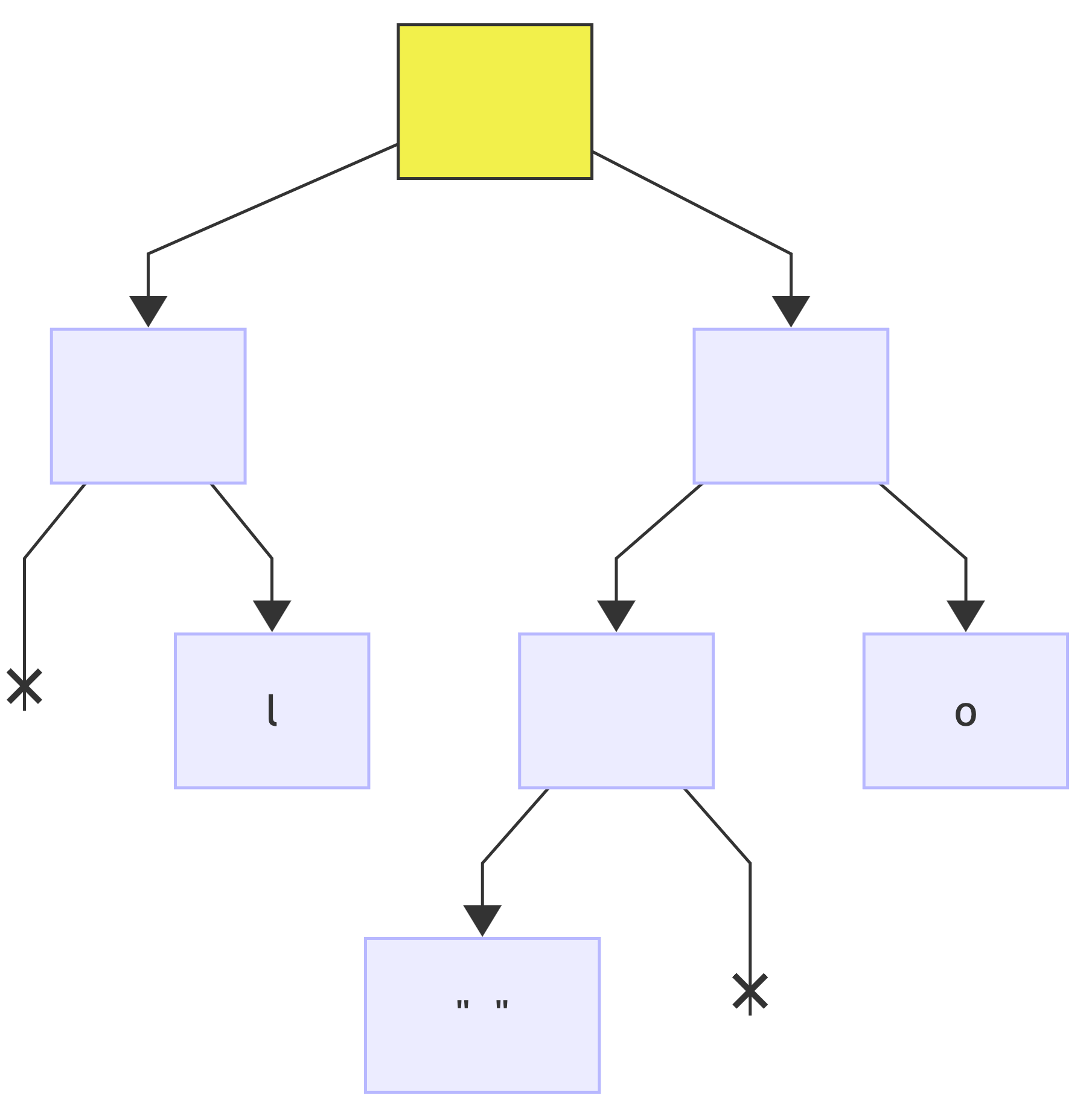
first bit is: 1, no changes to the tree since the node exists, just make it current (*):
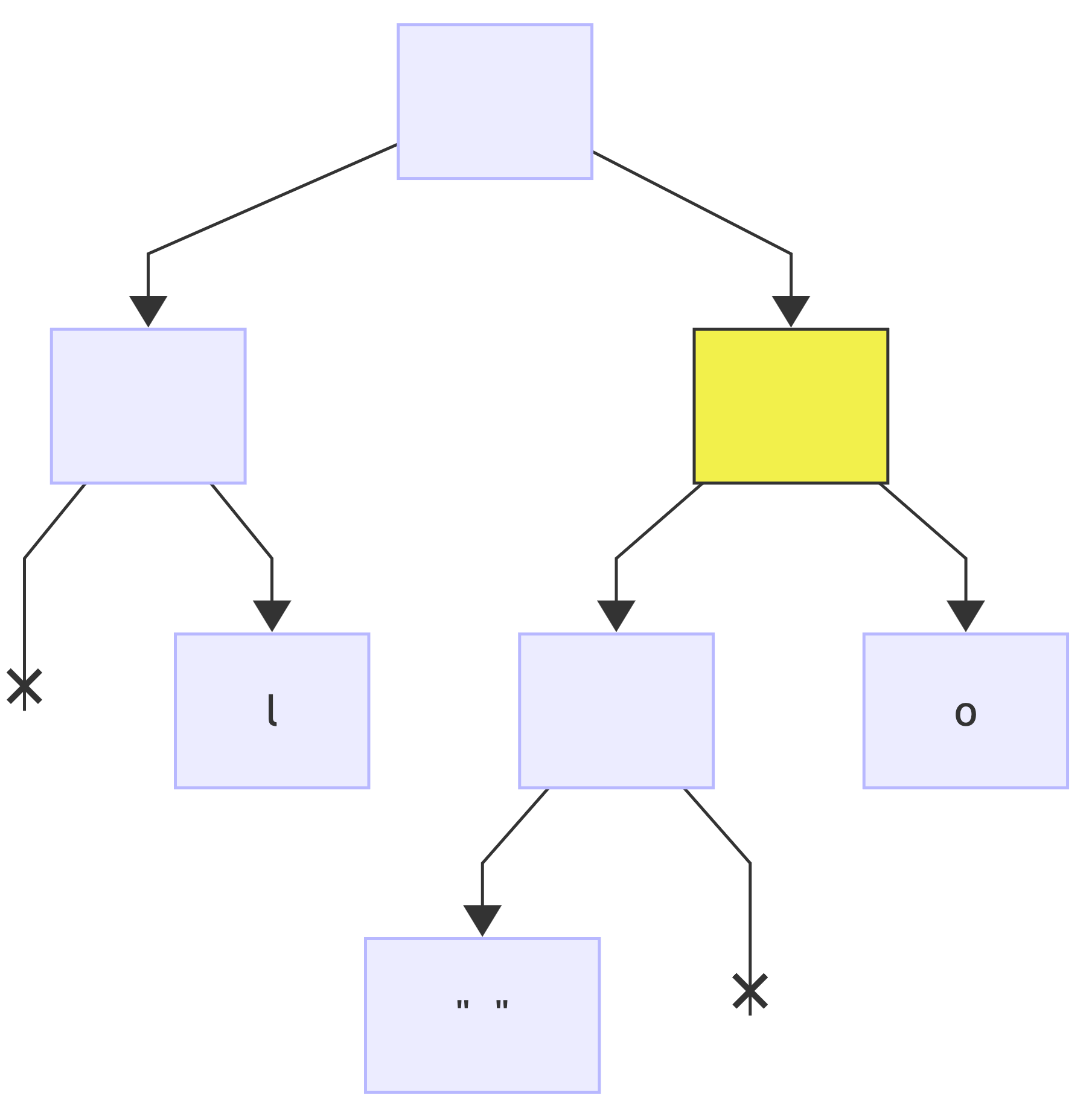
next bit is: 0, no changes to the tree since the node exists, just make it current (*):
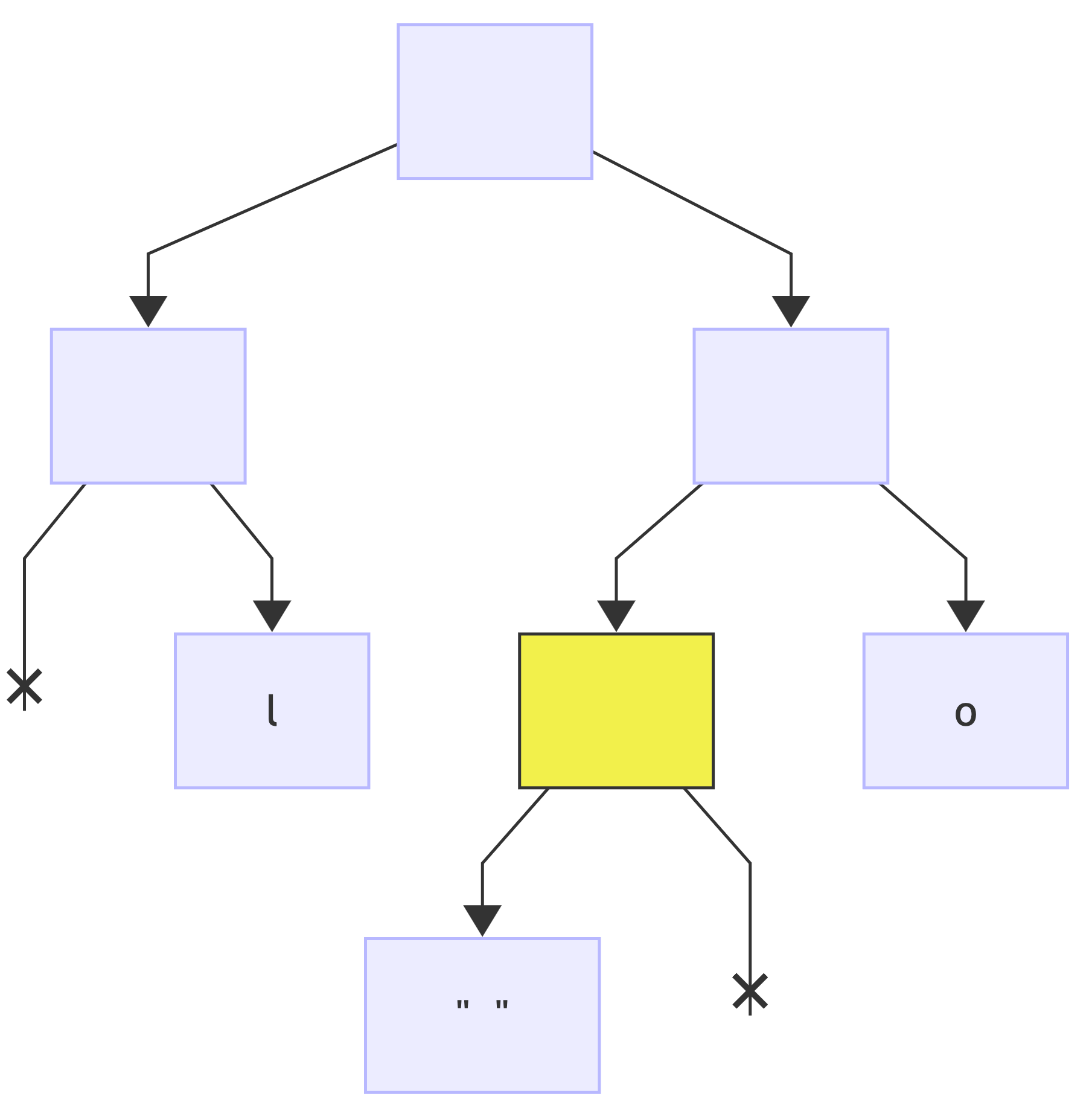
next bit is: 1, add a right child node and make it current (*):
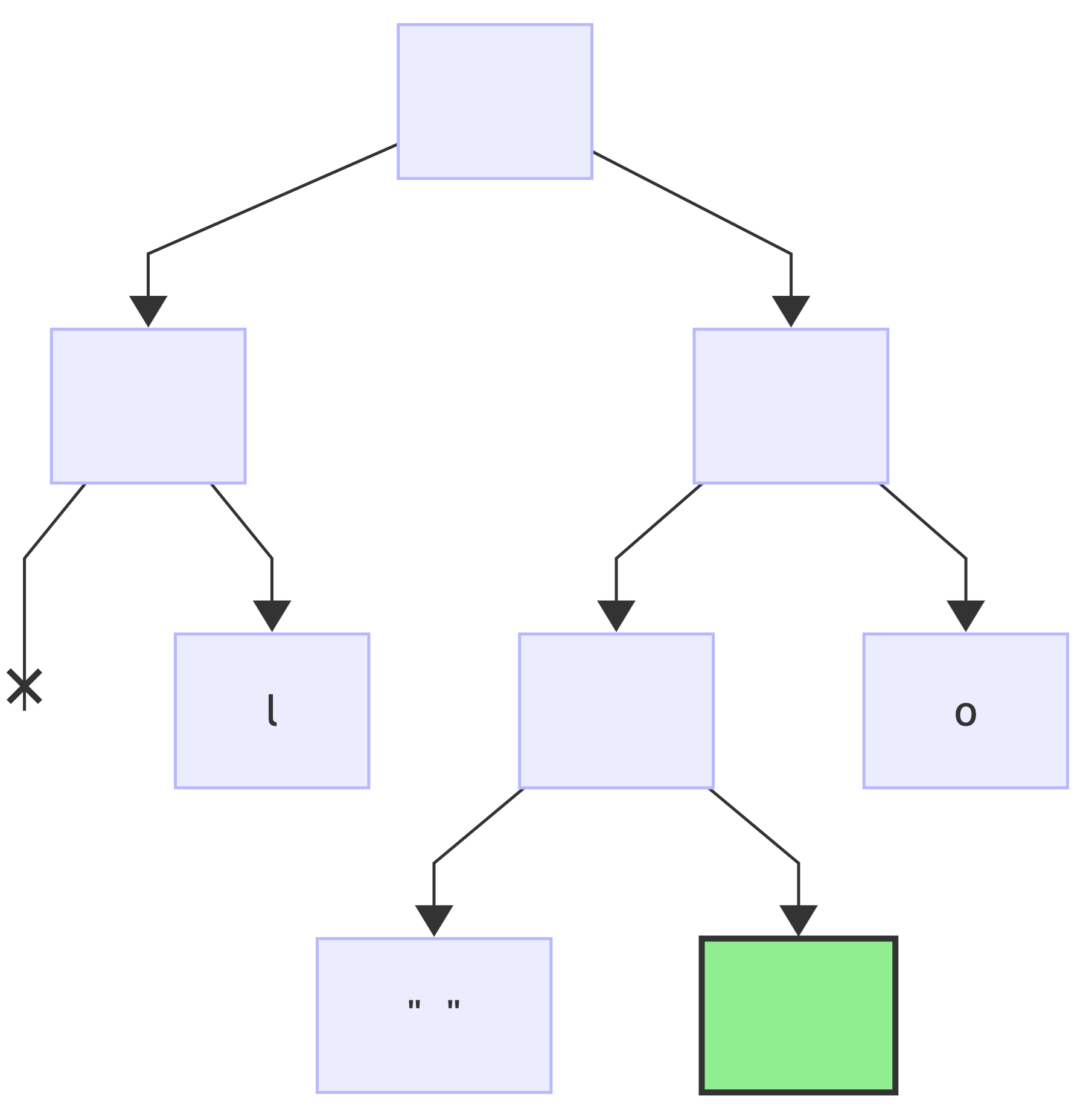
since this was the last bit, add a value to the current node:
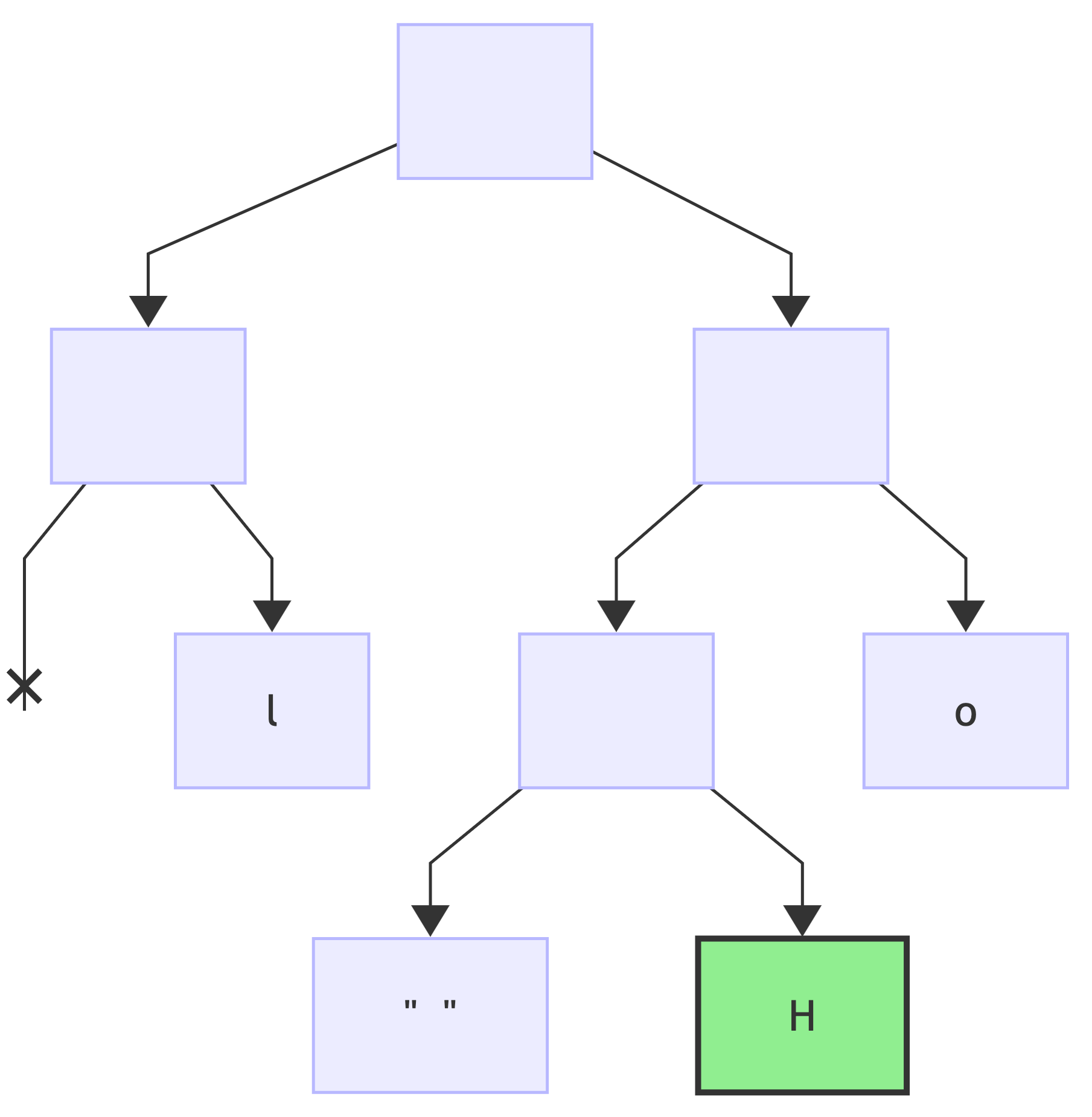
And without going step-by-step, for all the remaining encodings:
encoding: d => 0b0010:
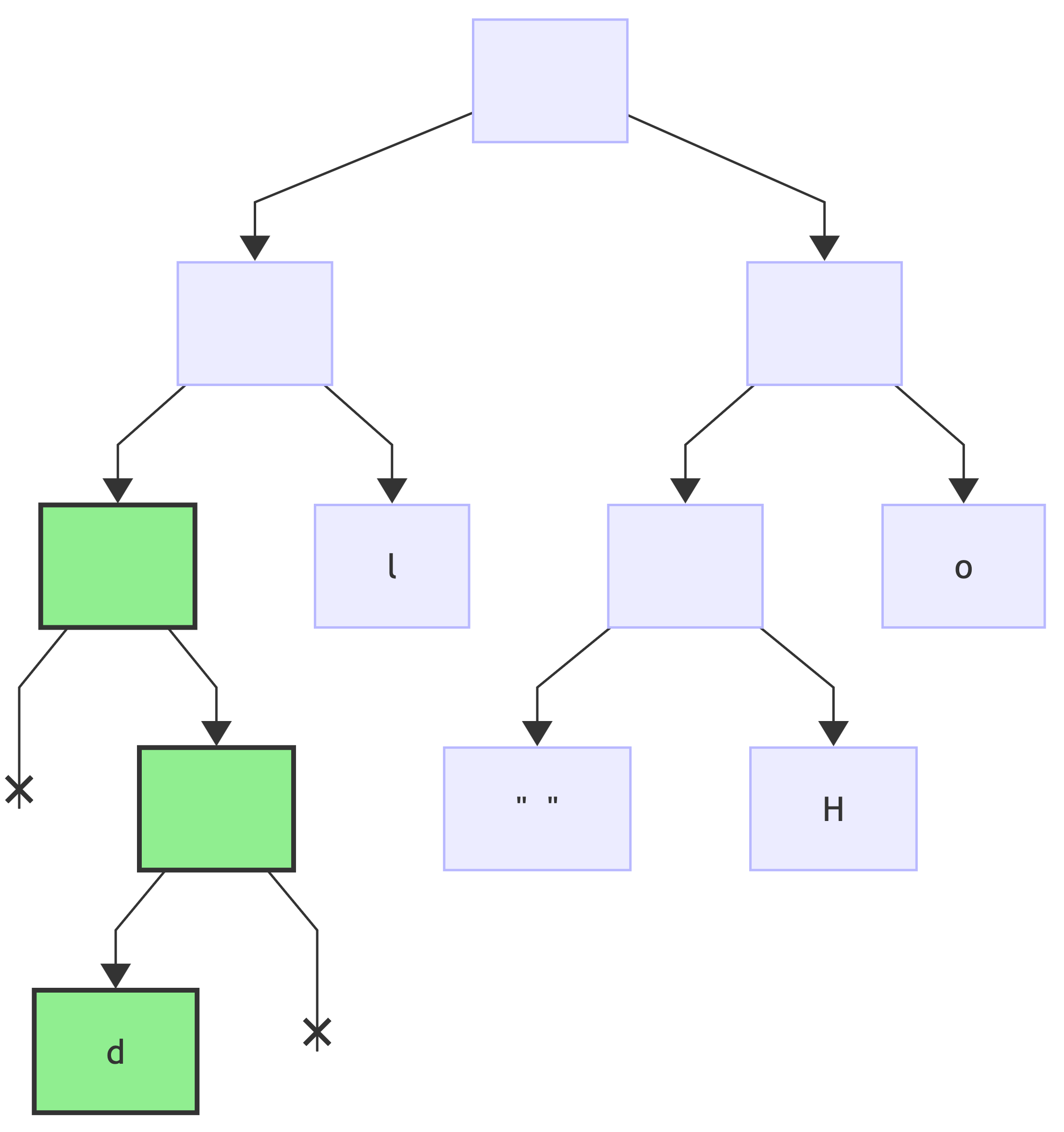
encoding: e => 0b0011:
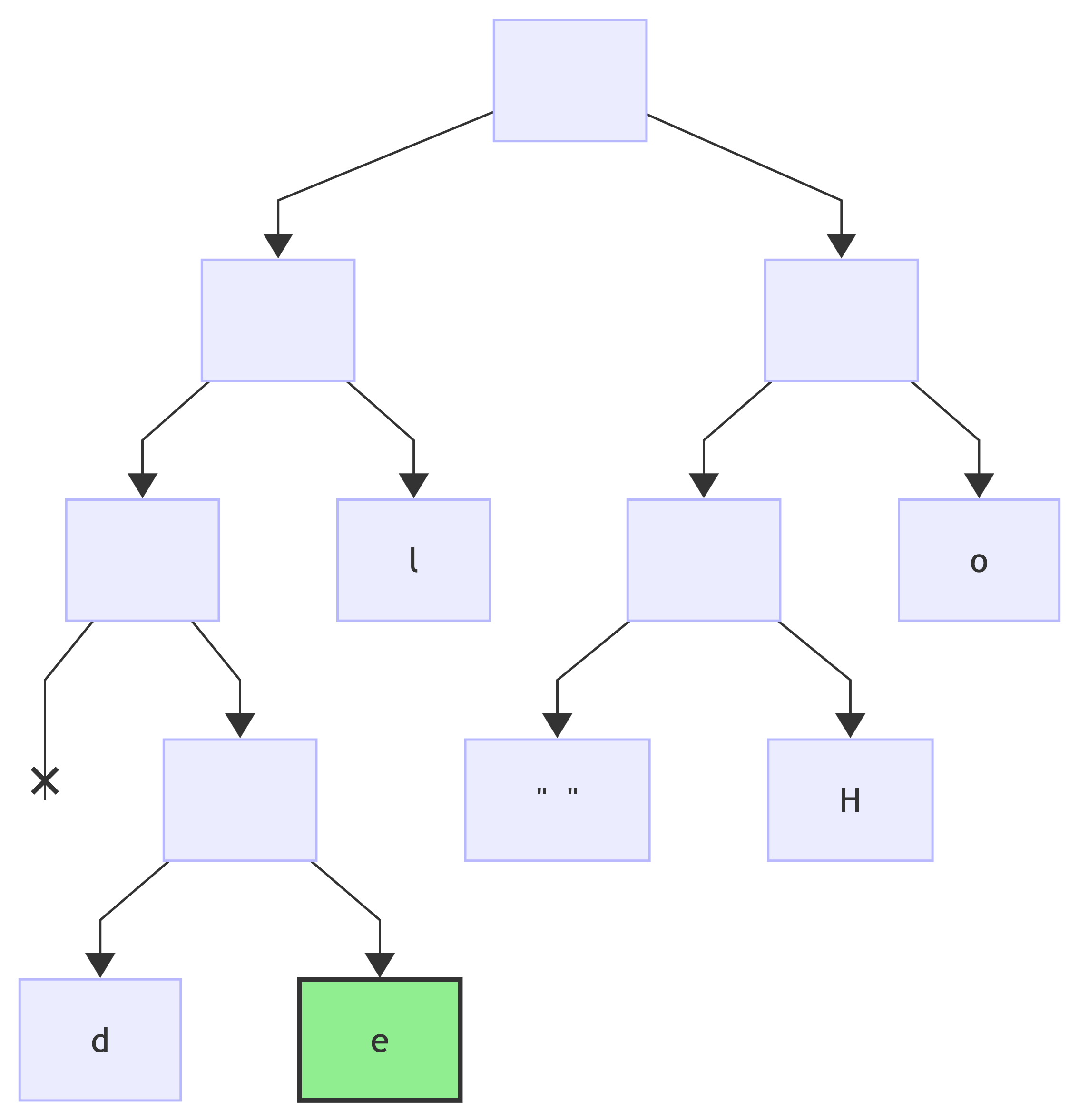
encoding: r => 0b0000:
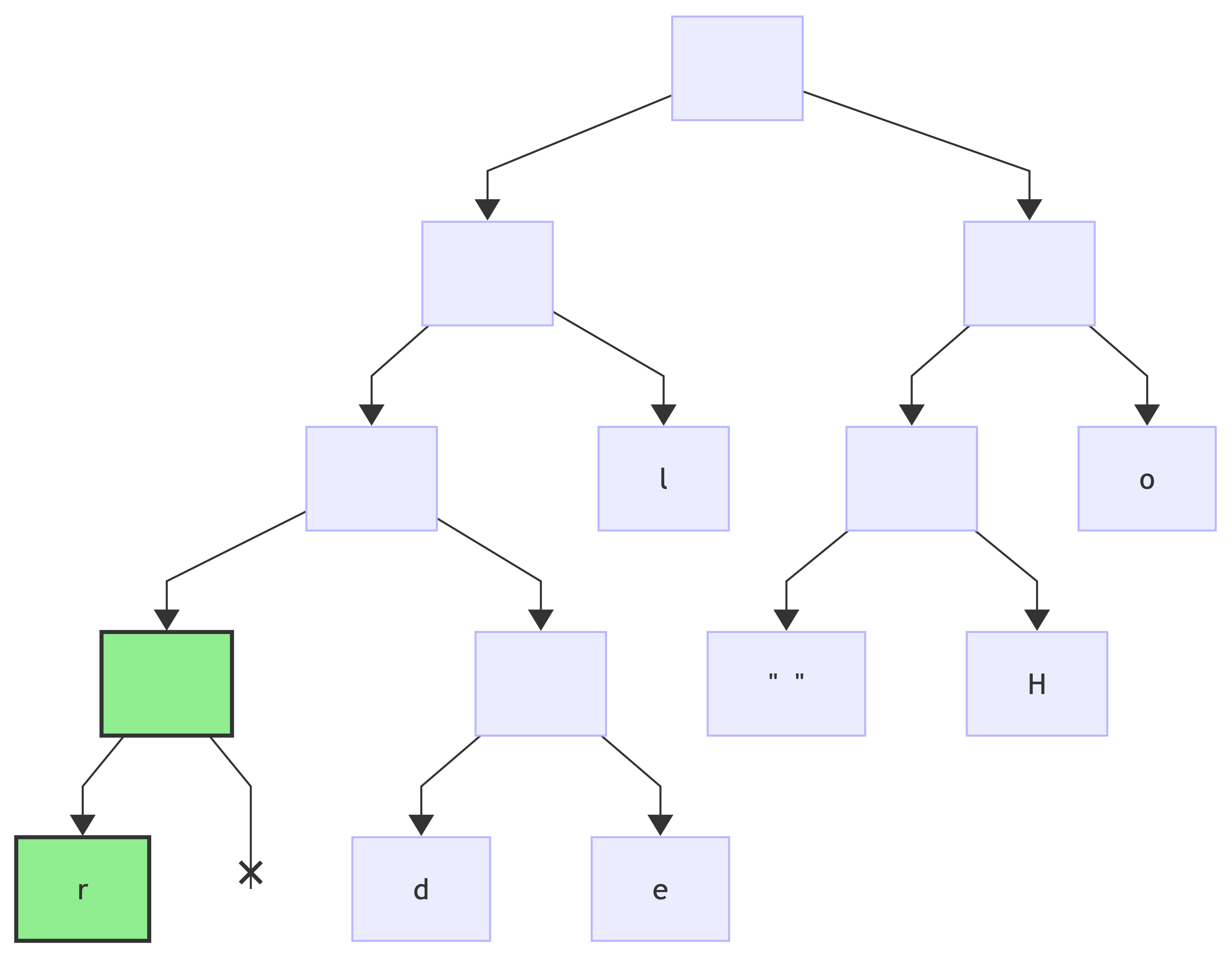
encoding: w => 0b0001:
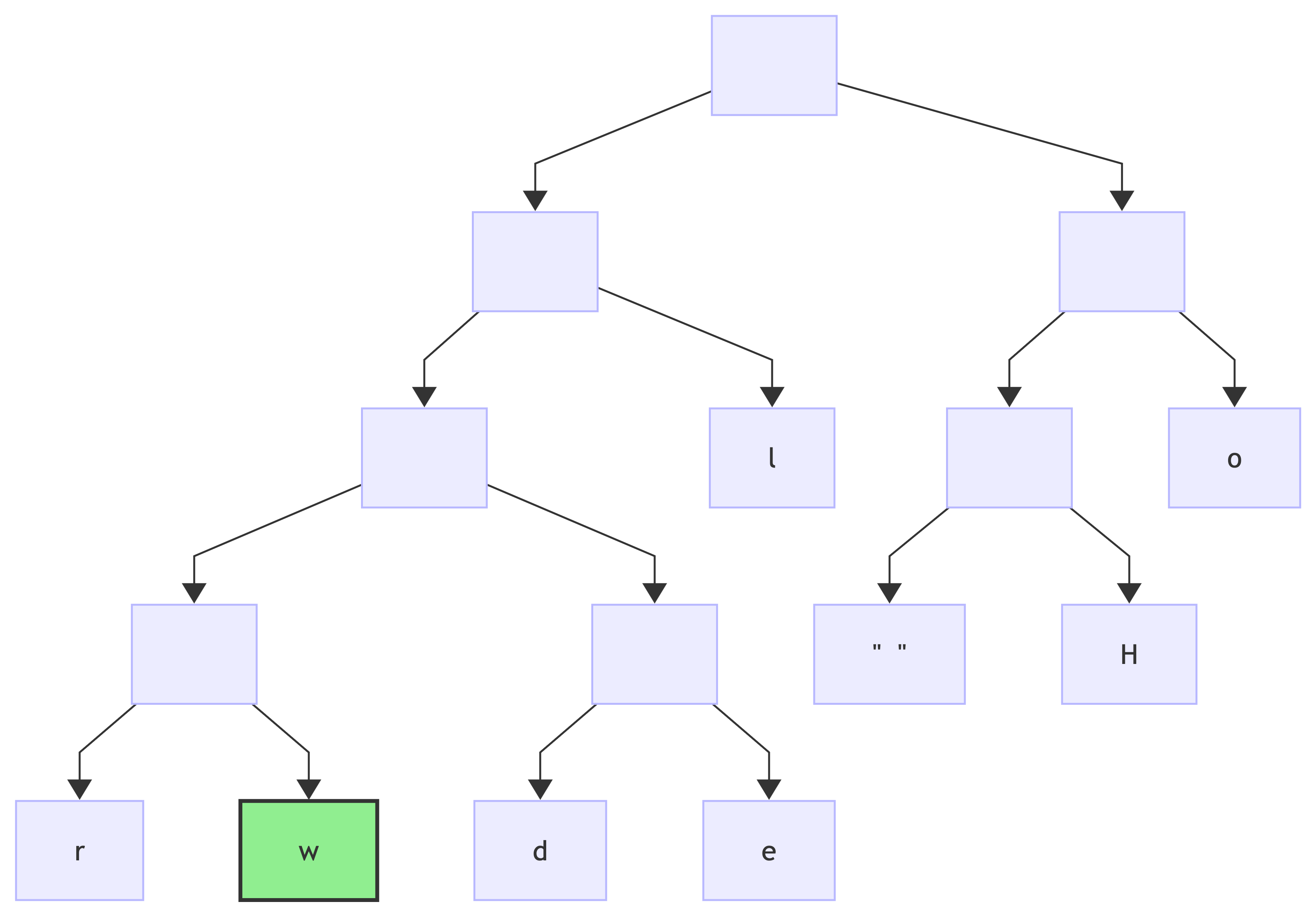
If the initial message (Hello world) is encoded with this algorithm (to four bytes: 0xA6 0xBC 0x1C 0x12), in order to properly decode it, the tree or the code table has to be given alongside with the encoded message:
message: 'Hello world' (11 bytes)
encoded: 0xA6 0xBC 0x1C 0x12 (4 bytes)
table: {"l"=>"01", "o"=>"11", " "=>"100", "H"=>"101", "r"=>"0000", "w"=>"0001", "d"=>"0010", "e"=>"0011"} (8 keys + 8 values = 16 bytes)
compression = 11 bytes -> 20 bytes = negative 100%
This is not entirely a compression algorithm, though. Algorithms such as ZIP (DEFLATE) and JPEG (although slightly different in details, the general approach still applicable) go further to compress the table itself. To understand how they work, one needs to understand the tricks behind them.
Canonical Huffman codes
There is one issue with just general Huffman encoding: there are multiple ways to build a different tree for the same input. Refer to the early stage of encoding from above:
(l, 3) (2) (o, 2) (2) (2)
/ \ / \ / \
(" ", 1) (H, 1) (d, 1) (e, 1) (r, 1) (w, 1)
Here's the non-deterministic part: which pair of nodes to merge next? Depending on the choice, the code for each character would be different (although the code length would remain the same).
That's where canonical Huffman codes come into play: this simple algorithm unifies the logic, transforming any valid Huffman tree for a given input into the same tree (so the codes remain the same).
To obtain canonical codes from any valid Huffman tree for a given input, the codes are transformed following two simple rules:
- sort the codes by code length (ascending) and then by character (also ascending)
- starting with
current_code = 0andcurrent_length = 0, iterate over each code length (assume iterator islength_i): - if the length is greater than
current_length, left shiftcurrent_codeby the differencelength_i - current_length - increment
current_code, filling the unused left-most bits with zeroes - update
current_lengthtolength_i
In the example above, the codes are:
l: 01
o: 11
" ": 100
H: 101
r: 0000
w: 0001
d: 0010
e: 0011
The lengths of those codes are:
l: 2 (Huffman code: '01', length of '01' = 2)
o: 2 (Huffman code: '11', length of '11' = 2)
" ": 3 (Huffman code: '100', length of '100' = 3)
H: 3 (Huffman code: '101', length of '101' = 3)
r: 4 (Huffman code: '0000', length of '0000' = 4)
w: 4 (Huffman code: '0001', length of '0001' = 4)
d: 4 (Huffman code: '0010', length of '0010' = 4)
e: 4 (Huffman code: '0011', length of '0011' = 4)
Making these codes canonical requires sorting by Huffman code's length first and then by character (I have left old codes in braces for reference):
l: 2 (old code: 01, its length = 2)
o: 2 (old code: 11, its length = 2)
" ": 3 (old code: 100, its length = 3)
H: 3 (old code: 101, its length = 3)
d: 4 (old code: 0010, its length = 4)
e: 4 (old code: 0011, its length = 4)
r: 4 (old code: 0000, its length = 4)
w: 4 (old code: 0001, its length = 4)
Then, re-assign codes, starting with 0 and padding to the length of old code:
l: 00 (old code length = 2, next code = 00 + 1 = 01)
o: 01 (old code length = 2, next code = 01 + 1 = 10)
" ": 100 (old code length = 3; but previous entry ('o' = 01) has length 2, so shift left by 1 bit ('10' << 1 == '100'); next code = 100 + 1 = 101)
H: 101 (old code length = 3; next code = 101 + 1 = 110)
d: 1100 (old code length = 4; but previous entry ('H' = 101) has length 3, so shift left by 1 bit ('110' << 1 == '1100'); next code = 1100 + 1 = 1101)
e: 1101 (old code length = 4; next code = 1101 + 1 = 1110)
r: 1110 (old code length = 4; next code = 1110 + 1 = 1111)
w: 1111 (old code length = 4)
Interestingly, this code did not use the previous codes themselves. This implies the codes could be calculated automatically if only the lengths of the codes are given.
For the example above, the encoding table is:
l: 00
o: 01
" ": 100
H: 101
d: 1100
e: 1101
r: 1110
w: 1111
Encoded message with this table looks like this:
message:
Hello world
encoded:
101 1101 00 00 01 100 1111 01 1110 00 1100
joined:
10111010000011001111011110001100
In Ruby:
def build_canonical_table(codes)
codes = codes.sort_by {|k, v| [v.length, k]}
canonical_codes = {}
curr_code = 0
prev_length = 0
codes.each do |char, old_code|
curr_code <<= (old_code.length - prev_length)
canonical_codes[char] = curr_code.to_s(2).rjust(old_code.length, '0')
curr_code += 1
prev_length = old_code.length
end
canonical_codes
endIn C++:
std::vector<std::pair<char, std::string>> sorted_codes(codes.begin(), codes.end());
std::sort(sorted_codes.begin(), sorted_codes.end(),
[](const auto& a, const auto& b) {
if (a.second.length() != b.second.length()) {
return a.second.length() < b.second.length();
}
return a.first < b.first;
});
std::map<char, std::string> canonical_codes;
int curr_code = 0;
int prev_length = 0;
for (auto [ch, code] : sorted_codes) {
curr_code <<= (code.length() - prev_length);
canonical_codes[ch] = std::bitset<32>(curr_code).to_string().substr(32 - code.length());
curr_code++;
prev_length = code.length();
}ZIP, DEFLATE
DEFLATE algorithm compresses the list of codes lengths using a constant table, defined by the standard (or algorithm description, if you will).
The constant table is defined in the archiver code itself, so it remains the same for all archives and does not need to be a part of archive itself.
The archive, on the other hand, stores a list of 256 values, each representing the length of the code of the corresponding character.
For example, archive may store a list like this:
0, 0, 2, 2, 4, 0, 0, 0, 0, ... (total 256 elements, all the rest are zeros)
But this is highly inefficient, so this list is also comressed using Huffman encoding. The difference is that this list is first compressed using run-length encoding (from the very top of this blog) and the result is compressed using the pre-defined Huffman table.
Step-by-step this looks like this: first, the original content is compressed. This produces a Huffman table.
Assume this table of canonical Huffman codes for input Hello world:
l : "00"
o : "01"
" ": "100"
H : "101"
d : "1100"
e : "1101"
r : "1110"
w : "1111"
As described above, for canonical Huffman codes, storing only codes' lengths is enough to reconstruct the codes:
"00" : 2
"01" : 2
"100" : 3
"101" : 3
"1100" : 4
"1101" : 4
"1110" : 4
"1111" : 4
So the table of codes' lengths looks like this:
1: 0 (codes of length 1: none)
2: 2 (codes of length 2: two codes)
3: 2 (codes of length 3: two codes)
4: 4 (codes of length 4: four codes)
This table looks very much like an indexed array (1-based, though - indexes start at 1 instead of 0 like in C), so it could be represented as an array.
Given this data, at any point Huffman codes could be re-created:
code = 0
// lengths: [0, 2, 2, 4]
length_i = 1, codes_length_i = 0;
no codes of length 1 => skip
length_i = 2, codes_length_i = 2;
code (0) << 1 => code = 00;
create <codes_length_i (2)> codes:
emit code (00), code += 1 (code = 01);
emit code (01), code += 1 (code = 10);
length_i = 3, codes_length_i = 2;
code (10) << 1 => code = 100;
create <codes_length_i (2)> codes:
emit code (100), code += 1 (code = 101)
emit code (101), code += 1 (code = 110);
length_i = 4, codes_length_i = 4;
code (110) << 1 => code = 1100;
create <codes_length_i (4)> codes:
emit code (1100), code += 1 (code = 1101);
emit code (1101), code += 1 (code = 1110);
emit code (1110), code += 1 (code = 1111);
emit code (1111), code += 1 (code = 10000);
So for the list of codes lengths [0, 2, 2, 4] the re-created codes will be
00
01
100
101
1100
1101
1110
1111
In Ruby:
def recreate_canonical_huffman_codes(codes_of_length)
code = 0
res = []
codes_of_length.each_with_index do |n, len|
code <<= 1
n.times do
res << code.to_s(2).rjust(len+1, '0')
code += 1
end
end
res
endFor the second phase, the original symbols have to be correlated with these codes somehow. DEFLATE does not store the symbols or their corresponding encodings at any point - instead it uses smart algorithm to encode the encodings (so meta!) for all possible symbols.
Referring back to the compressed content's table of codes:
l : "00" (code length: 2)
o : "01" (code length: 2)
" ": "100" (code length: 3)
H : "101" (code length: 3)
d : "1100" (code length: 4)
e : "1101" (code length: 4)
r : "1110" (code length: 4)
w : "1111" (code length: 4)
In a similar manner to codes lengths' table, a table of all possible 256 byte values (ASCII table, effectively) is created and the corresponding byte's code length is written to this table:
0x00: 0
0x01: 0
0x02: 0
...
0x20 (" "): 3
...
0x48 (H) : 3
...
0x64 (d) : 4
0x65 (e) : 4
...
0x6c (l) : 2
...
0x6f (o) : 2
...
0x72 (r) : 4
...
0x77 (w) : 4
...
Instead of hexadecimal values, here's decimal representation:
32 (" ") : 3
72 (H) : 3
100 (d) : 4
101 (e) : 4
108 (l) : 2
111 (o) : 2
114 (r) : 4
119 (w) : 4
This list could be written as follows:
index: [0, 1, 2, 3, 4, ..., 31, 32, 33, 34, 35, ..., 71, 72, 73, ..., 99, 100, 101, 102, ..., 108, ..., 111, 112, 113, 114, ..., 119, ..., 255 ]
value: [0, 0, 0, 0, 0, ..., 0, 3, 0, 0, 0, ..., 0, 3, 0, ..., 0, 4, 4, 0, ..., 2, ..., 2, 0, 0, 4, ..., 4, ..., 0 ]
This list contains a lot of duplications and a lot of zeroes. It is then compressed using the run-length algorithm (from the very top of this blog), which now makes sense:
(0, 32), (3, 1), (0, 39), (3, 1), (0, 27), (4, 1), (4, 1), (0, 6), (2, 1), (0, 2), (2, 1), (0, 2), (4, 1), (0, 4), (4, 1), (0, 136)
But DEFLATE does it smarter - it uses pre-defined table of symbols, again:
- for zero value, use zero itself
- for values 1..15, use the value itself as a code
- to repeat previous value 3..6 times, use code
16and3extra bits to represent how many repetitions (000- repeat previous value 3 times,001- repeat previous value 4 times,010- repeat previous value 5 times,011- repeat previous value 6 times) - to repeat value
03..10 times, use code17and extra bits - to repeat value
011..138 times, use code18and extra bits
And then DEFLATE compresses the table of codes' lenghts with Huffman encoding.
Since there is a very limited number of characters to encode (1..15, 16, 17, 18 - 19 values total), the maximum code length, even if all of these values were used, would be about 4 bits.
The values 16, 17 and 18 will always be followed by a pre-defined number of bits (extra bits describing a parameter), so when decoding, if the value decoded is one of those three (16, 17 or 18), the following pre-defined number of bits are interpreted differently.
Look at this process step-by-step. First, the code lenghts array is replaced with the codes from above using run-length algorithm:
Repeated zeros are represented by following this simple table:
- single zero:
0 - two zeros:
0, 0(two zero bytes) - 3..10 zeros:
17followed by0for 3 zeros1for 4 zeros2for 5 zeros- etc.
7for 10 zeros
- 11..138 zeros:
18followed by0for 11 zeros1for 12 zeros- etc.
127for 138 zeros
These extra bits are not encoded using Huffman codes. The rest of the codes (raw values 0..15, 16, 17, 18) are encoded according to their frequencies.
(0, 32) -> 18 (repeat '0' 32 times), followed by extra bits representing 32 repetition: 32 - 11 = 21 (0b00010101)
(3, 1) -> 3
(0, 39) -> 18 (repeat '0' 39 times), followed by extra bits representing 39 repetitions: 39 - 11 = 28 (0b00011100)
(3, 1) -> 3
(0, 27) -> 18 (repeat '0' 27 times), followed by extra bits representing 27 repetitions: 27 - 11 = 16 (0b00010000)
(4, 1) -> 4
(4, 1) -> 4
(0, 6) -> 17 (repeat '0' 6 times), followed by extra bits representing 6 repetitions: 6 - 3 = 3 (0b00000011)
(2, 1) -> 2
(0, 2) -> [0, 0]
(2, 1) -> 2
(0, 2) -> [0, 0]
(4, 1) -> 4
(0, 4) -> 17 (repeat '0' 4 times), followed by extra bits representing 4 repetitions: 4 - 3 = 1 (0b00000001)
(4, 1) -> 4
(0, 136) -> 18 (repeat '0' 136 times), followed by extra bits representing 136 repetitions: 136 - 11 = 125 (0b01111101)
After this, the codes lengths list becomes:
18, 21 (0b00010101), 3, 18, 28 (0b00011100), 3, 18, 16 (0b00010000), 4, 4, 17, 3 (0b00000011), 2, 0, 0, 2, 0, 0, 4, 17, 1 (0b00000001), 4, 18, 125 (0b01111101)
In Ruby:
def running_codes_lengths(codes)
codes_lengths = (0..255).map {|i| (codes[i.chr] || '').length}
result = []
i = 0
while i < codes_lengths.size
len = codes_lengths[i]
run_length = 1
while i + run_length < codes_lengths.size && codes_lengths[i + run_length] == len
run_length += 1
end
i += run_length
if len == 0
while run_length > 0
if run_length >= 11
# code 18, repeat '0' 11..138 times
diff = [138, [11, run_length].max].min
result << [18, diff - 11]
run_length -= diff
elsif run_length >= 3
# code 17, repeat '0' 3..10 times
diff = [10, [3, run_length].max].min
result << [17, diff - 3]
run_length -= diff
else
result += [0] * run_length
run_length = 0
end
end
elsif len != 0 && run_length >= 3
result << len
run_length -= 1
while run_length > 0
# code 16, repeat previous value 3..6 times
diff = [6, [3, run_length].max].min
result << [16, diff - 3]
run_length -= diff
end
else
run_length.times { result << len }
run_length = 0
end
end
result
endIn C++:
struct CodeLengthNode {
size_t length;
int extra_bits;
};
std::vector<CodeLengthNode*> code_lengths;
for (auto i = 0; i < 256; i++) {
auto length = canonical_codes[i].length();
auto run_length = 1;
while (i + run_length < 256 && canonical_codes[i + run_length].length() == length) {
run_length++;
}
i += run_length - 1;
if (length == 0) {
while (run_length > 0) {
if (run_length >= 11) {
// code 18, repeat '0' 11..138 times
auto diff = std::min(138, std::max(11, run_length));
code_lengths.push_back(new CodeLengthNode{ .length = 18, .extra_bits = diff - 11 });
run_length -= diff;
}
else if (run_length >= 3) {
// code 17, repeat '0' 3..10 times
auto diff = std::min(10, std::max(3, run_length));
code_lengths.push_back(new CodeLengthNode{ .length = 17, .extra_bits = diff - 3 });
run_length -= diff;
}
else {
for (auto t = 0; t < run_length; t++) {
code_lengths.push_back(new CodeLengthNode{ .length = 0, .extra_bits = 0 });
}
run_length = 0;
}
}
}
else if (length != 0 && run_length >= 3) {
code_lengths.push_back(new CodeLengthNode{ .length = length, .extra_bits = 0 });
run_length--;
while (run_length > 0) {
auto diff = std::min(6, std::max(3, run_length));
code_lengths.push_back(new CodeLengthNode{ .length = 16, .extra_bits = diff - 3 });
run_length -= diff;
}
}
else {
for (auto t = 0; t < run_length; t++) {
code_lengths.push_back(new CodeLengthNode{ .length = length, .extra_bits = 0 });
}
run_length = 0;
}
}To compress this list, ignore the extra bits and count values 0..18 only:
18, 21, 3, 18, 28, 3, 18, 16, 4, 4, 17, 3, 2, 0, 0, 2, 0, 0, 4, 17, 1, 4, 18, 125
without extra bit values:
18, 3, 18, 3, 18, 16, 4, 4, 17, 3, 2, 0, 0, 2, 0, 0, 4, 17, 1, 4, 18
counts:
18 : 4
3 : 3
16 : 1
4 : 4
17 : 2
2 : 2
0 : 4
1 : 1
Next, order these mappings by count, followed by the number itself (key of this dictionary / hashmap):
0 : 4
4 : 4
18 : 4
3 : 3
2 : 2
17 : 2
1 : 1
16 : 1
Then, create Huffman tree for these counts:
step 1:

step 2:
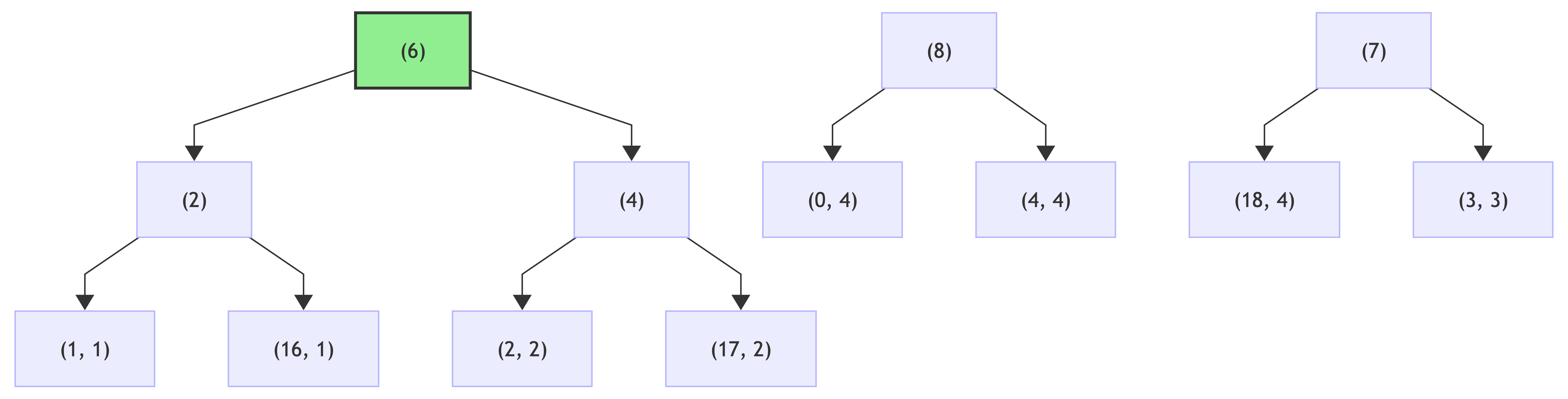
step 3:
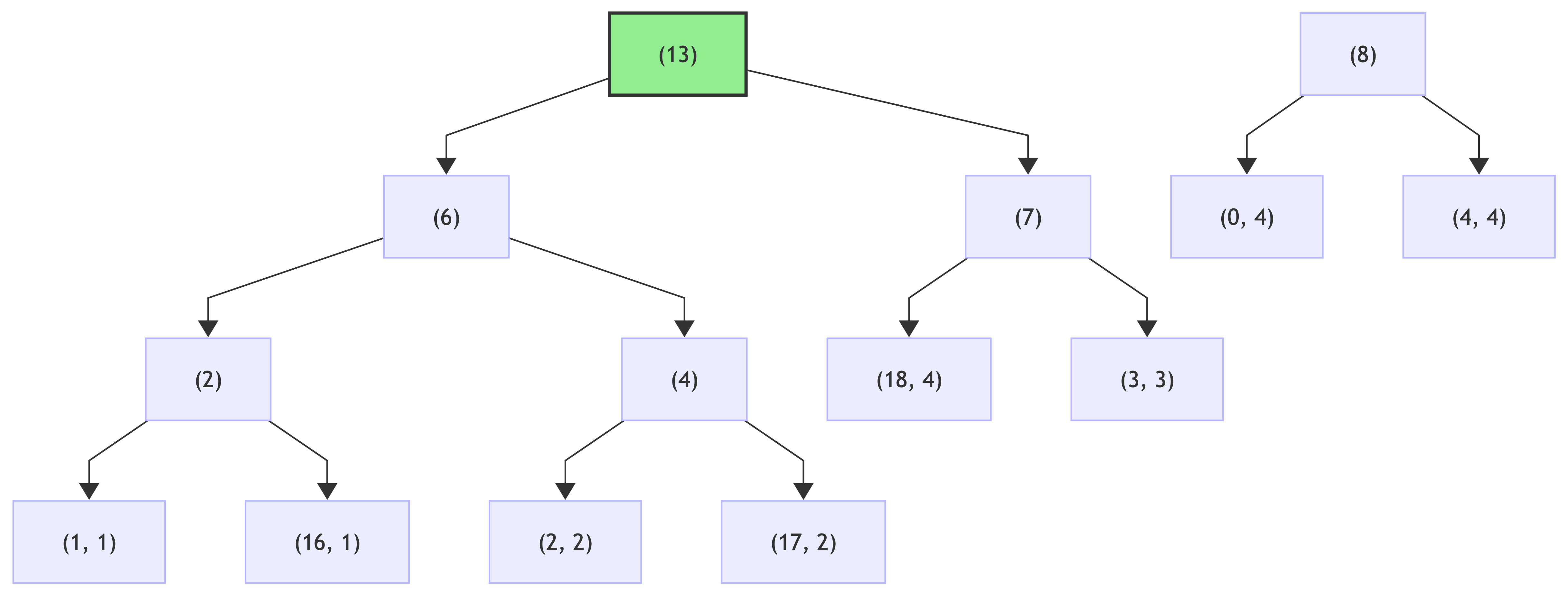
step 4:
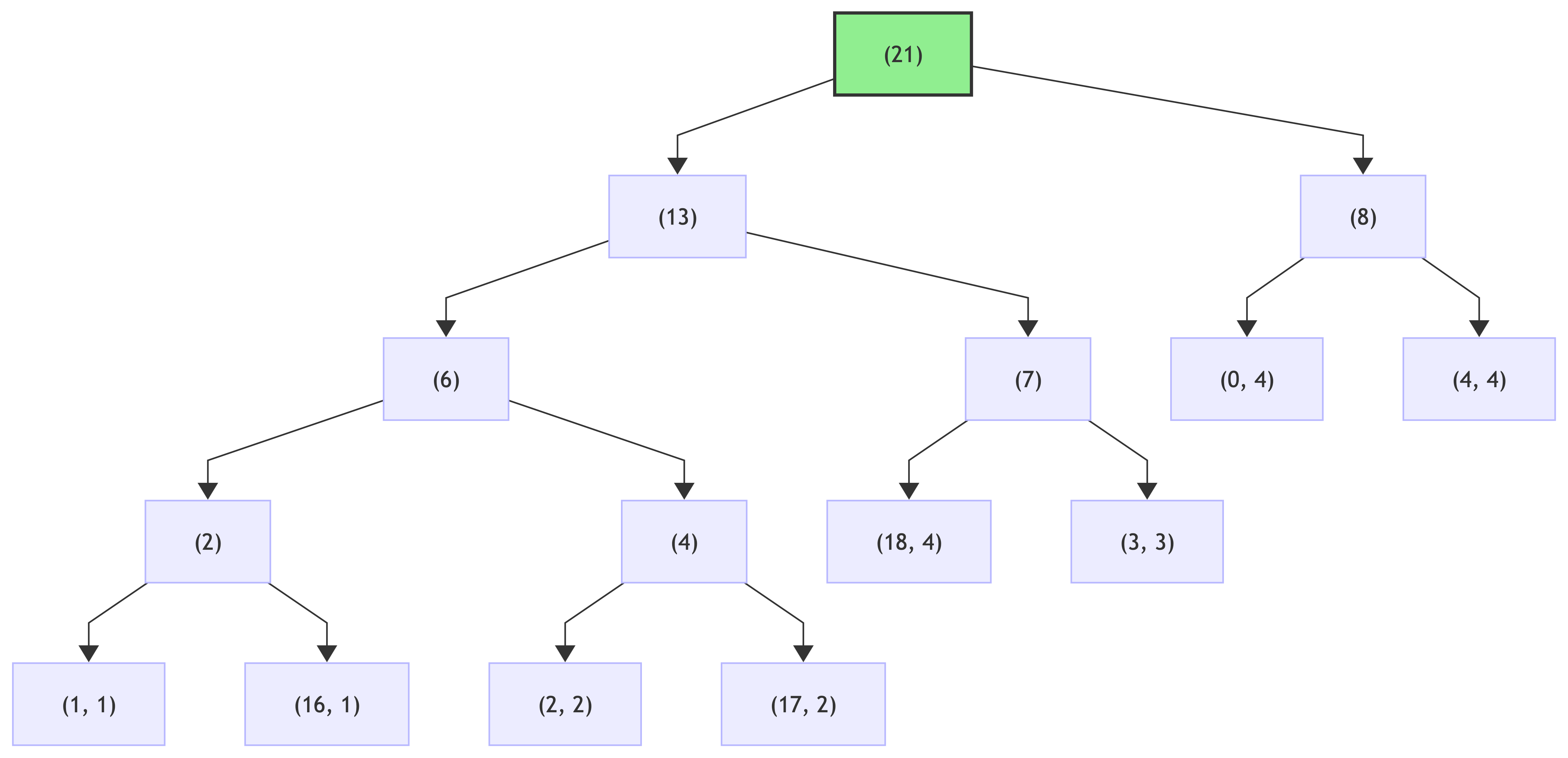
Following the rule "left branch => 0, right branch => 1", traverse the tree and assign codes to each leaf node:
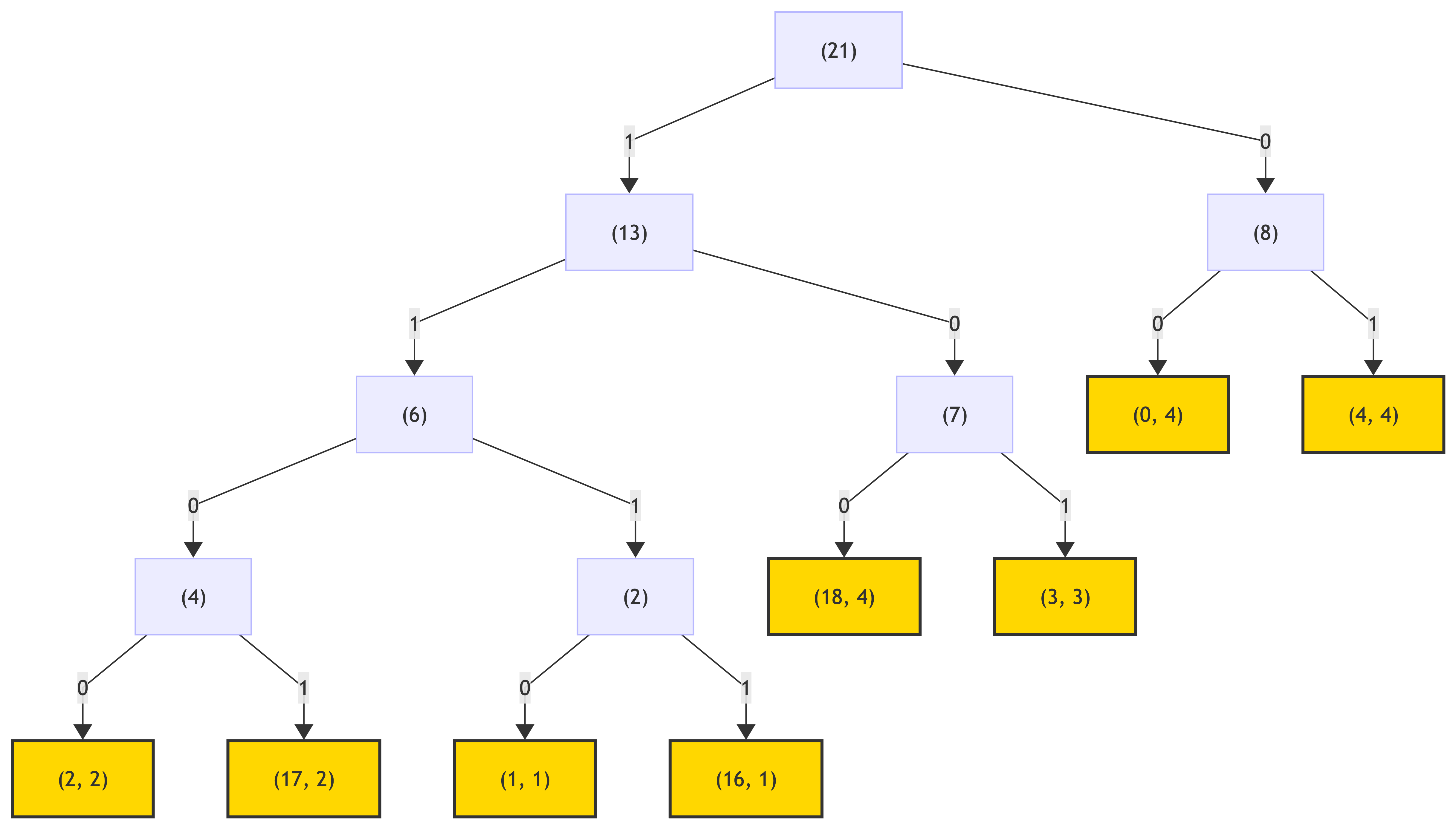
This yields:
(0, 4, 00) (4, 4, 01) (18, 4, 100) (3, 3, 101) (2, 2, 1100) (17, 2, 1101) (1, 1, 1110) (16, 1, 1111)
or
0 (4 occurrences) : 00
4 (4 occurrences) : 01
18 (4 occurrences) : 100
3 (3 occurrences) : 101
2 (2 occurrences) : 1100
17 (2 occurrences) : 1101
1 (1 occurrences) : 1110
16 (1 occurrences) : 1111
Then, assign the canonical Huffman codes:
step 1: sort codes by lengths and code itself:
0 : 00 (code length: 2)
4 : 01 (code length: 2)
18 : 100 (code length: 3)
3 : 101 (code length: 3)
2 : 1100 (code length: 4)
17 : 1101 (code length: 4)
1 : 1110 (code length: 4)
16 : 1111 (code length: 4)
becomes
0 : 00 (code length: 2)
4 : 01 (code length: 2)
3 : 101 (code length: 3)
18 : 100 (code length: 3)
1 : 1110 (code length: 4)
2 : 1100 (code length: 4)
16 : 1111 (code length: 4)
17 : 1101 (code length: 4)
step 2: assign incrementing and shifting code:
code = 0, previous_length = 0
0 : 00 (code length: 2), code = 00, next code = 01
4 : 01 (code length: 2), code = 01, next code = 10
3 : 101 (code length: 3), length > previus_length => shift code, code = 100, next code = 101
18 : 100 (code length: 3), code = 101, next code = 110
1 : 1110 (code length: 4), length > previous_length => shift code, code = 1100, next code = 1101
2 : 1100 (code length: 4), code = 1101, next code = 1110
16 : 1111 (code length: 4), code = 1110, next code = 1111
17 : 1101 (code length: 4), code = 1111
Going back to what the initial codes' lengths list was (the thing being encoded):
18, 21 (0b00010101), 3, 18, 28 (0b00011100), 3, 18, 16 (0b00010000), 4, 4, 17, 3 (0b00000011), 2, 0, 0, 2, 0, 0, 4, 17, 1 (0b00000001), 4, 18, 125 (0b01111101)
Now encoded with this new Huffman encoding:
100, 00010101, 101, 100, 00011100, 101, 100, 1111, 00010000, 01, 01, 1101, 101, 00000011, 1100, 00, 00, 1100, 00, 00, 01, 1101, 1110, 00000001, 01, 100, 01111101
joined:
1000001010110110000011100101100111100010000010111011010000001111000000110000000111011110000000010110001111101
And the tree for this encoding could be just a list of 19 elements (one for each code used in this code lengths encoding) of codes lengths (for the encoded code lengths list):
0 : 00 (code length: 2)
4 : 01 (code length: 2)
3 : 101 (code length: 3)
18 : 100 (code length: 3)
1 : 1110 (code length: 4)
2 : 1100 (code length: 4)
16 : 1111 (code length: 4)
17 : 1101 (code length: 4)
simplified:
0 : 2
1 : 4
2 : 4
3 : 3
4 : 2
16 : 4
17 : 4
18 : 3
becomes
index: [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 ]
value: [ 2, 4, 4, 3, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 4, 3 ]
or just
2, 4, 4, 3, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 4, 3
Note one interesting observation: since there is a very limited number of symbols used to encode code lengths, the maximum code for them is 7, which is 3 bits long. This means the new encodings for code lengths table could be packed into 3 bit chunks, further reducing the size of this tree:
codes lengths (for codes lengths, so meta!):
2, 4, 4, 3, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 4, 3
encoded into binary:
010, 100, 100, 011, 010, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 100, 100, 011
joined:
010100100011010000000000000000000000000000000000100100011
Now, build the header for the archive, consisting of code lengths encoded with DEFLATE:
code lengths tree:
010100100011010000000000000000000000000000000000100100011
code lengths for each character, encoded:
1000001010110110000011100101100111100010000010111011010000001111000000110000000111011110000000010110001111101
in bytes:
01010010 01110100 00000000 00000000 00000000 00000000 10010001 11000001 01001011 00000111 00101100 11110001 00000101 11011010 00000111 10000001 10000000 11101111 00000000 10110001 111101
in hex:
0x52 0x74 0x00 0x00 0x00 0x00 0x91 0xC1 0x4B 0x07 0x2C 0xF1 0x05 0xDA 0x07 0x81 0x80 0xEF 0x00 0xB1 0x3D
And build the content of the archive, which is just the encoded message (from a while ago):
encoded message:
10111010000011001111011110001100
in bytes:
10111010 00001100 11110111 10001100
in hex:
0xBA 0x0C 0xF7 0x8C
Joining header and the body:
0x52 0x74 0x00 0x00 0x00 0x00 0x91 0xC1 0x4B 0x07 0x2C 0xF1 0x05 0xDA 0x07 0x81 0x80 0xEF 0x00 0xB1 0x3D 0xBA 0x0C 0xF7 0x8C
Funny enough, the length of this archive is much longer than the original message itself - 25 bytes vs original 11 - more than negative 100% increase in size.
But the important part is that this is due to the fact that the message is short and most symbols only occur once.
On a longer text the compression is actually good: a typical AI response compression:
Source length: 3994
Encoded length: 2632
> encoded length: 2573
> header length: 59
>> header1 length: 8
>> header2 length: 51
Compression rate: 51%
Decoding works the same three-step way, just in the reverse:
- decode canonical Huffman tree for codes' lengths
- decode codes' lengths and build the canonical Huffman tree again
- decode the message using that tree
The only tricky part there is decoding the codes' lengths, since it involves re-building the symbols + extra bits for repeated values.
Decoding codes' lengths:
def decode_code_lengths_lengths(header)
bits = header.bytes.map {|ch| ch.to_s(2).rjust(8, '0')}.join
code_lengths = []
(0..18).each do |e|
start_bit = e * 3
three_bits = bits[start_bit, 3]
length = three_bits.to_i(2)
code_lengths[e] = length
end
code_lengths
endThen the canonical Huffman codes are reconstructed for decoding next stage of codes' lengths:
def recreate_huffman_codes(code_lengths)
symbols_with_lengths = code_lengths.each_with_index.filter {|len, _| len > 0}.map {|len, s| [s, len] }.sort_by {|s, len| [len, s]}
res = Array.new(code_lengths.size)
prev_length = 0
code = 0
symbols_with_lengths.each do |s, len|
code <<= (len - prev_length)
res[s] = code.to_s(2).rjust(len, '0')
code += 1
prev_length = len
end
res
endThis is then used to decode running lengths (compressed lengths):
def decode_compressed_code_lengths(bits, codes_lengths_tree)
tree_inv = codes_lengths_tree.each_with_index.to_h
compressed_code_lengths = []
bit_pos = 0
buf = ''
decoded_count = 0
while bit_pos < bits.length && decoded_count < 256
buf += bits[bit_pos]
bit_pos += 1
if tree_inv.key?(buf)
symbol = tree_inv[buf]
buf = ''
case symbol
when 16
extra_bits = bits[bit_pos, 2].to_i(2)
bit_pos += 2
compressed_code_lengths << [16, extra_bits]
decoded_count += 3 + extra_bits # code 16 repeats 3-6 repetitions
when 17
extra_bits = bits[bit_pos, 3].to_i(2)
bit_pos += 3
compressed_code_lengths << [17, extra_bits]
decoded_count += 3 + extra_bits # code 17 repeats 3-10 repetitions
when 18
extra_bits = bits[bit_pos, 7].to_i(2)
bit_pos += 7
compressed_code_lengths << [18, extra_bits]
decoded_count += 11 + extra_bits # code 18 repeats 11-138 repetitions
else
compressed_code_lengths << symbol
decoded_count += 1 # any other code adds 1 instance of itself
end
end
end
compressed_code_lengths
endWhich is then used to reconstruct all codes' lengths for all symbols:
def decode_running_lengths(compressed_code_lengths)
res = []
compressed_code_lengths.each do |e|
if e.is_a?(Array)
code, extras = e
case code
when 16
repeats = 3 + extras
repeats.times { res << res.last }
when 17
repeats = 3 + extras
repeats.times { res << 0 }
when 18
repeats = 11 + extras
repeats.times { res << 0 }
end
else
res << e
end
end
res
endThese last two methods are there just to showcase the same process as encoding, but in reverse. Practically speaking, it does not make sense to build the intermediate running lengths encoding (with codes 16, 17 and 18) and the actual list could be built in-place:
def decode_codes_lengths(header, codes_lengths_tree)
bits = header.bytes.map {|b| b.to_s(2).rjust(8, '0')}.join
tree_inv = codes_lengths_tree.each_with_index.to_h
bit_pos = 0
buf = ''
res = []
while bit_pos < bits.length && res.size < 256
buf += bits[bit_pos]
bit_pos += 1
if tree_inv.key?(buf)
symbol = tree_inv[buf]
buf = ''
case symbol
when 16
extra_bits = bits[bit_pos, 2].to_i(2)
bit_pos += 2
repeats = 3 + extra_bits
repeats.times { res << res.last }
when 17
extra_bits = bits[bit_pos, 3].to_i(2)
bit_pos += 3
repeats = 3 + extra_bits
repeats.times { res << 0 }
when 18
extra_bits = bits[bit_pos, 7].to_i(2)
bit_pos += 7
repeats = 11 + extra_bits
repeats.times { res << 0 }
else
res << symbol
end
end
end
res
endThis list is then used to create the ultimate canonical Huffman codes for the message itself (the "body" of the archive), by calling recreate_huffman_codes:
def decode(header1, header2, body)
code_lengths_lengths = decode_code_lengths_lengths(header1)
tree = recreate_huffman_codes(code_lengths_lengths)
codes_lengths = decode_codes_lengths(header2, tree)
codes = recreate_huffman_codes(codes_lengths)
decode_body(body, codes)
endDecoding the body with this tree is simple:
def decode_with_tree(bits, tree)
tree_inv = tree.each_with_index.to_h
res = []
buf = ''
bits.each_char do |bit|
buf += bit
if tree_inv.key? buf
res << tree_inv[buf]
buf = ''
end
end
res
end
def decode_body(body, codes_lengths)
bits = body.bytes.map {|b| b.to_s(2).rjust(8, '0')}.join
bytes = decode_with_tree(bits, codes_lengths)
bytes.pack('C*').force_encoding('UTF-8')
endNote how these methods use string.bytes instead of string.chars - this is to make the algorithm work with UTF-8 characters and not only ASCII.
For binary data it can be hit or miss. For example, a PNG is already a compressed binary data, so DEFLATE does not prove too useful:
Raw data (PNG file): 2356 bytes
Encoded: 2397 bytes
Compression ratio: -1%
For a larger uncompressed data (so potentially more of the same characters being used more frequently), like a TTF font:
Raw data (TTF font): 7316 bytes
Encoded: 5161 bytes
Compression ratio: 29%
JPEG, DHT
Define Huffman Table uses a much simpler approach - it stores the list of codes lengths using an index-as-value approach - a list of 16 values effectively translated as "element at index 'i' tells how many codes of length 'i' are there in the table". This list is followed by the list of raw characters used in the message.
For example, an array like this
[0, 0, 2, 2, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
is expanded like so:
index: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
value: [0, 0, 2, 2, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
codes of length 0: 0
codes of length 1: 0
codes of length 2: 2
codes of length 3: 2
codes of length 4: 4
codes of length 5: 0
codes of length 6: 0
codes of length 7: 0
codes of length 8: 0
codes of length 9: 0
codes of length 10: 0
codes of length 11: 0
codes of length 12: 0
codes of length 13: 0
codes of length 14: 0
codes of length 15: 0
For the Hello world message, the archive header, comprising of codes' lengths and the alphabet, would look as following:
canonical Huffman codes:
l: 00 (length: 2)
o: 01 (length: 2)
" ": 100 (length: 3)
H: 101 (length: 3)
d: 1100 (length: 4)
e: 1101 (length: 4)
r: 1110 (length: 4)
w: 1111 (length: 4)
number of codes per length:
[ 0, 0, 2, 2, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
alphabet (in order same order as canonical Huffman codes table):
[ l, o, " ", H, d, e, r, w ]
Followed by the encoded message, the entire archive would look like this:
codes per length:
[ 0, 0, 2, 2, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
in bytes:
0x00 0x00 0x02 0x02 0x04 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
alphabet:
[ l, o, " ", H, d, e, r, w ]
in bytes:
0x6C 0x6F 0x20 0x48 0x64 0x65 0x72 0x77
encoded message:
10111010000011001111011110001100
in bytes:
0xBA 0x0C 0xF7 0x8C
combined:
0x00 0x00 0x02 0x02 0x04 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x6C 0x6F 0x20 0x48 0x64 0x65 0x72 0x77 0xBA 0x0C 0xF7 0x8C
The total length is 28, almost triple the original length!
Implementing this in Ruby:
# using the three helpers from the previous implementations - build_tree, build_table, build_canonical_table
def build_canonical_codes(message)
build_canonical_table(build_table(build_tree(message.bytes)))
end
def encode(message)
codes = build_canonical_codes(message)
grouped_codes = codes.values.group_by { |code| code.length }
codes_count_by_length = grouped_codes.transform_values { |cs| cs.size }
header1 = (1..15).map { |len| codes_count_by_length[len] || 0 }
header2 = codes.keys
body = message.bytes.map { |byte| codes[byte] }.join.chars.each_slice(8).map { |slice| slice.join.ljust(8, '0').to_i(2) }
{
header1: header1,
header2: header2,
body: body
}
endThen, the final message would be comprised of joining those parts together:
r = encode('Hello world')
[ :header1, :header2, :body ].map { |k| r[k].pack('C*').force_encoding('UTF-8') }.joinAs I said before, for a simple message such as Hello world the archive is 27 bytes long, which is longer than the original data itself.
But for something longer, like the AI chatbot response from before it is actually a bit better:
Original message: 3994
Encoded message: 2598
> header1: 15
> header2: 90
> body: 2573
Compression ratio: 49%
Decoding this is much simpler than DEFLATE: all there is to do is to reconstruct canonical Huffman codes from the number of codes by length (16-element-array)
# using `recreate_huffman_codes` helper from before
# decode_with_table is slightly different from decode_with_tree
def decode_with_table(bits, table)
res = []
buf = ''
bits.each_char do |bit|
buf += bit
if table.key? buf
res << table[buf]
buf = ''
end
end
res
end
def decode(message)
bytes = message.bytes
counts_encoded = bytes[0, 15]
counts = counts_encoded.each_with_index.map { |n, len| [ len + 1 ] * n }.flatten
codes = recreate_huffman_codes count
symbols = bytes[15, codes.size]
table = codes.zip(symbols).to_h
body_encoded = bytes[15 + codes.size ..]
body_bits = body_encoded.map { |b| b.to_s(2).rjust(8, '0') }.join
body_decoded = decode_with_table(body_bits, table)
body_decoded.pack('C*').force_encoding('UTF-8')
endBy the way, all the code in this blog is available in a separate repo.
This algorithm works much worse with binary data, however:
Raw data (PNG file): 2356 bytes
Encoded: 2605 bytes
Compression ratio: -2%
On a larger uncompressed binary data (same TTF font as before):
Raw data (TTF font): 7316 bytes
Encoded: 5336 bytes
Compression ratio: 27%