Floyd-Warshall algorithm, revised
In this blog I would like to brush upon Floyd-Warshall algorithm implementation I have described previously.
See, generally, when explaining Floyd-Warshall algorithm, the graph is given as an adjacency matrix - an V x V matrix, where V is the number of vertices (nodes) in a graph and each matrix value representing the distance between each vertex.
For instance, the value G[1][3] = 12 represents the edge from vertex 1 to vertex 3 with the value of 12.
Aside from adjacency matrix, there are two other common ways to represent a graph:
- incidence matrix of size
V x EforVvertices andEedges, where each row represents an edge value (G[i][j] > 0for edgei -> j,G[i][j] < 0for edgej -> i,G[i][j] = 0for no edge between verticesiandj) - adjacency list, where each vertex is represented as an object with a list of its connections
Consider the graph from the previous blog:
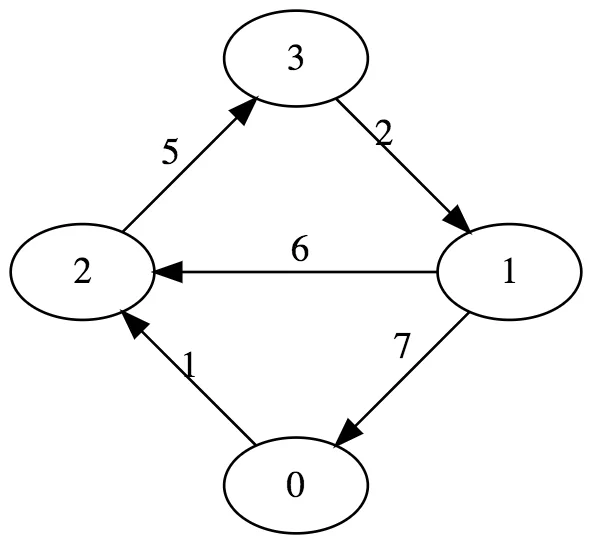
It can be represented in three different ways:
adjacency list:
v0: [ [2 -> 1] ]
v1: [ [2 -> 6], [0 -> 7] ]
v2: [ [3 -> 5] ]
v3: [ [1 -> 2] ]
adjacency matrix:
| v0 v1 v2 v3
---+------------------
v0 | 0 0 1 0
v1 | 7 0 6 0
v2 | 0 0 0 5
v3 | 0 2 0 0
incidence matrix:
| e0 e1 e2 e3 e4
---+---------------------
v0 | 0 0 0 7 0
v1 | 0 0 2 0 0
v2 | 1 0 0 0 6
v3 | 0 5 0 0 0
However, arguably the most common and most memory-efficient way to represent graph in a real-world application would be the adjacency list.
Hence I thought a bit of a revised implementation is needed, since the previous one (aka "classic" implementation) relies on matrices.
And those matrices contain quite a bit of unused data. Take the graph above as an example: it has 4 vertices and 5 edges.
An adjacency matrix would use 16 numbers, incidence matrix would use 20 numbers and adjacency list would use 5 tuples of 2 numbers (10 numbers, so to speak).
"Classic" Floyd-Warshall algorithm implementation constructs an additional matrix for the shortest paths' distances (at most it can reuse the existing one representing the graph itself) and an additional V x V matrix for path reconstruction.
With a graph represented as an adjacency list (or just a list of node objects), the algorithm can use something like a dictionary (or a hashmap) to reduce the memory consumption. Subjectively, it also becomes easier to read and understand the algorithm.
First, we'd need few definitions:
class Node
{
public string Name;
public Dictionary<Node, int> Connections;
public Node(string name)
{
this.Name = name;
this.Connections = new Dictionary<Node, int>();
}
public override string ToString()
{
return this.Name;
}
}
class Graph
{
public List<Node> Nodes;
public Graph()
{
this.Nodes = new List<Node>();
}
}
class Path
{
public Node From;
public Node To;
public List<Node> Nodes;
public int Distance;
public Path(Node from, Node to)
{
this.Distance = 0;
this.From = from;
this.To = to;
this.Nodes = new List<Node>();
}
}The Path class is a bit excessive, as it really only needs a list of Node objects, but I decided to make it verbose on purpose - to make it easier to debug.
The algorithm then becomes like this:
Dictionary<(Node from, Node to), Node> FindAllPaths(Graph g)
{
var distance = new Dictionary<(Node from, Node to), int>();
var pathThrough = new Dictionary<(Node from, Node to), Node>();
foreach (var nodeFrom in g.Nodes)
{
foreach (var nodeTo in g.Nodes)
{
if (nodeFrom == nodeTo)
{
distance.Add((nodeFrom, nodeTo), 0);
}
else
{
distance.Add((nodeFrom, nodeTo), int.MaxValue);
}
}
foreach (var nodeTo in nodeFrom.Connections.Keys)
{
distance[(nodeFrom, nodeTo)] = nodeFrom.Connections[nodeTo];
pathThrough.Add((nodeFrom, nodeTo), nodeTo);
}
pathThrough.Add((nodeFrom, nodeFrom), nodeFrom);
}
foreach (var nodeThrough in g.Nodes)
{
foreach (var nodeFrom in g.Nodes)
{
foreach (var nodeTo in g.Nodes)
{
if (nodeFrom == nodeTo || distance[(nodeThrough, nodeTo)] == int.MaxValue || distance[(nodeFrom, nodeThrough)] == int.MaxValue)
{
continue;
}
if (distance[(nodeFrom, nodeTo)] > distance[(nodeFrom, nodeThrough)] + distance[(nodeThrough, nodeTo)])
{
distance[(nodeFrom, nodeTo)] = distance[(nodeFrom, nodeThrough)] + distance[(nodeThrough, nodeTo)];
pathThrough[(nodeFrom, nodeTo)] = pathThrough[(nodeFrom, nodeThrough)];
}
}
}
}
return pathThrough;
}One can easily see the separate parts of the algorithm - initializing the intermediate storage (for the paths and distances) and actually finding the shortest paths. It is pretty much the same algorithm as before with the only difference being the use of dictionary instead of a matrix.
Path reconstruction bit is also a little bit different (not too much though):
Path ReconstructPath(Node from, Node to, Dictionary<(Node from, Node to), Node> allPaths)
{
if (!allPaths.ContainsKey((from, to)))
{
return null;
}
var path = new Path(from, to);
var tempNode = from;
path.Nodes.Add(tempNode);
while (tempNode != to)
{
var nextNode = allPaths[(tempNode, to)];
path.Distance += tempNode.Connections[nextNode];
path.Nodes.Add(nextNode);
tempNode = nextNode;
}
return path;
}Now, there is one major improvement we can make to this algorithm. See, when we initialize the dictionaries for paths and distances, we follow the same logic as with the classic implementation, putting in the values for edges which do not exist in a graph:
foreach (var nodeFrom in g.Nodes)
{
// this bit will add entries for inexistent edges
foreach (var nodeTo in g.Nodes)
{
if (nodeFrom == nodeTo)
{
distance.Add((nodeFrom, nodeTo), 0);
}
else
{
distance.Add((nodeFrom, nodeTo), int.MaxValue);
}
}
// ...
}But as a matter of fact, we do not really have to store these values - instead, we could simply have a check whether the needed entry exists in the dictionary or not:
Dictionary<(Node from, Node to), Node> FindAllPaths(Graph g)
{
var distance = new Dictionary<(Node from, Node to), int>();
var pathThrough = new Dictionary<(Node from, Node to), Node>();
foreach (var nodeFrom in g.Nodes)
{
// -- no more unnecessary entries --
foreach (var nodeTo in nodeFrom.Connections.Keys)
{
distance.Add((nodeFrom, nodeTo), nodeFrom.Connections[nodeTo]);
pathThrough.Add((nodeFrom, nodeTo), nodeTo);
}
pathThrough.Add((nodeFrom, nodeFrom), nodeFrom);
}
foreach (var nodeThrough in g.Nodes)
{
foreach (var nodeFrom in g.Nodes)
{
foreach (var nodeTo in g.Nodes)
{
if (nodeFrom == nodeTo)
{
continue;
}
// ++ but one extra check here, to prevent unnecessary iterations ++
if (!distance.ContainsKey((nodeFrom, nodeThrough)) || !distance.ContainsKey((nodeThrough, nodeTo)))
{
continue;
}
// ++ and one extra check here, to annotate the existence of a new, indirect shortest path between nodeFrom and nodeTo ++
if (!distance.ContainsKey((nodeFrom, nodeTo)) || distance[(nodeFrom, nodeTo)] > distance[(nodeFrom, nodeThrough)] + distance[(nodeThrough, nodeTo)])
{
distance[(nodeFrom, nodeTo)] = distance[(nodeFrom, nodeThrough)] + distance[(nodeThrough, nodeTo)];
pathThrough[(nodeFrom, nodeTo)] = pathThrough[(nodeFrom, nodeThrough)];
}
}
}
}
return pathThrough;
}For that matter, we don't really need to have a separate dictionary for path reconstruction - since both distance and pathThrough dictionaries serve the same purpose (have the exact same key, but different value), we can smash those two together and use even less memory:
Dictionary<(Node from, Node to), (Node through, int distance)> FindAllPaths(Graph g)
{
var pathThrough = new Dictionary<(Node from, Node to), (Node through, int distance)>();
foreach (var nodeFrom in g.Nodes)
{
foreach (var nodeTo in nodeFrom.Connections.Keys)
{
pathThrough.Add((nodeFrom, nodeTo), (nodeTo, nodeFrom.Connections[nodeTo]));
}
pathThrough.Add((nodeFrom, nodeFrom), (nodeFrom, 0));
}
foreach (var nodeThrough in g.Nodes)
{
foreach (var nodeFrom in g.Nodes)
{
foreach (var nodeTo in g.Nodes)
{
if (nodeFrom == nodeTo)
{
continue;
}
if (!pathThrough.ContainsKey((nodeFrom, nodeThrough)) || !pathThrough.ContainsKey((nodeThrough, nodeTo)))
{
continue;
}
if (!pathThrough.ContainsKey((nodeFrom, nodeTo)) || pathThrough[(nodeFrom, nodeTo)].distance > pathThrough[(nodeFrom, nodeThrough)].distance + pathThrough[(nodeThrough, nodeTo)].distance)
{
pathThrough[(nodeFrom, nodeTo)] = (nodeThrough, pathThrough[(nodeFrom, nodeThrough)].distance + pathThrough[(nodeThrough, nodeTo)].distance);
}
}
}
}
return pathThrough;
}Essentially, nothing special - just using the tuples for both the intermediate node and the distance for the shortest paths.
And with a tiny bit of a change, path reconstruction:
Path ReconstructPath(Node from, Node to, Dictionary<(Node from, Node to), (Node through, int distance)> allPaths)
{
if (!allPaths.ContainsKey((from, to)))
{
return null;
}
var path = new Path(from, to);
var tempNode = from;
path.Nodes.Add(tempNode);
while (tempNode != to)
{
var (nextNode, distance) = allPaths[(tempNode, to)];
path.Distance += distance;
path.Nodes.Add(nextNode);
tempNode = nextNode;
}
return path;
}