Floyd-Warshall algorithm
Update
There is a revised version of this blog, showing how an algorithm implementation could be optimized.
The story behind this post
Recently I've received +10 karma on StackOverflow. I was curious for what question or answer and clicked to check this. It appeared
to be a seven-year-old answer about a Floyd-Warshall algorithm. I was surprised with both my bad English (back those days...) and the very small value the answer had. So I've revised it and here it is -- the brand-new version!
The definitions
Let us have a graph, described by matrix D, where D[i][j] is the length of the edge (i -> j) (from graph's vertex with index i to the vertex with index j).
Matrix D has the size of N * N, where N is a total number of vertices in a graph because we can reach the maximum of paths by connecting each graph's vertex to each other.
Also, we'll need matrix R, where we will store the vertices of the shortest paths (R[i][j] contains the index of a vertex, where the shortest path from vertex i to vertex j lies).
Matrix R has the same size as D.
The Floyd-Warshall algorithm performs these steps:
-
initialize the matrix of all the paths between any two pairs of vertices in a graph with the edge's end vertex (this is important since this value will be used for path reconstruction)
-
for each pair of connected vertices (read: for each edge
(u -> v)),uandv, find the vertex, which forms shortest path between them: if the vertexkdefines two valid edges(u -> k)and(k -> v)(if they are present in the graph), which are together shorter than path(u -> v), then assume the shortest path betweenuandvlies throughk; set the shortest pivot point in matrixRfor edge(u -> v)to be the corresponding pivot point for edge(u -> k)
But how do we read the matrix D?
Inputs
Take sample graph:
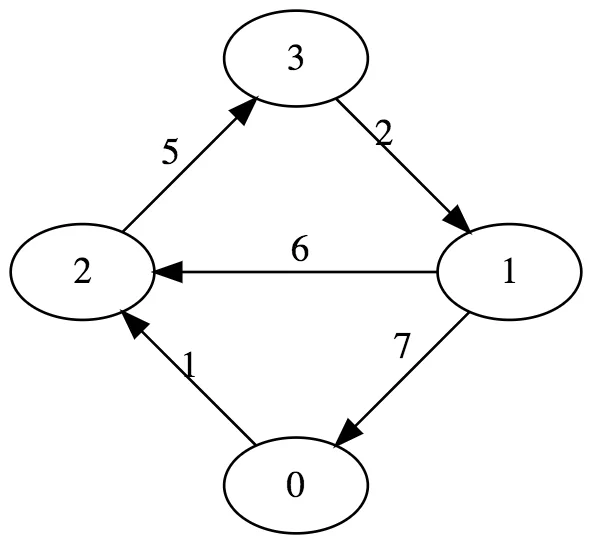
In GraphViz it would be described as follows:
digraph G {
layout = "circo";
0->2 [label = "1"];
2->3 [label = "5"];
3->1 [label = "2"];
1->2 [label = "6"];
1->0 [label = "7"];
}
We first create a two-dimensional array of size 4 (since there are exactly 4 vertices in our graph).
We initialize its main diagonal (the items, whose indices are equal, for ex. G[0, 0], G[1, 1], etc.) with zeros, because
the shortest path from vertex to itself has the length 0 and the other elements with a very large number (to indicate there is no edge or an infinitely long edge between them). The defined elements, corresponding to graph's edges, we fill with edges' lengths:
int N = 4;
int[,] D = new int[N, N];
for (int i = 0; i < N; i++) {
for (int t = 0; t < N; t++) {
if (i == t) {
D[i, t] = 0;
} else {
D[i, t] = 9999;
}
}
}And let's say we initialize our D matrix by hand:
D[0, 2] = 1;
D[1, 0] = 7;
D[1, 2] = 6;
D[2, 3] = 5;
D[3, 1] = 2;The algorithm itself
Now that we are on a same page with definitions, algorithm can be implemented like this:
int[,] R = new int[N, N];
// Initialise the routes matrix R, essentially saying "the shortest path from u to v is straight"
for (int i = 0; i < N; i++) {
for (int t = 0; t < N; t++) {
R[i, t] = t;
}
}
// Floyd-Warshall algorithm; note the order of iterators DOES matter:
for (int k = 0; k < N; k++) {
for (int u = 0; u < N; u++) {
for (int v = 0; v < N; v++) {
// check if the shortest path from "u" to "v" is actually through "k"
if (D[u, v] > D[u, k] + D[k, v]) {
D[u, v] = D[u, k] + D[k, v];
R[u, v] = R[u, k];
}
}
}
}Let's "animate" this algorithm in few steps for the sample graph from above:
Initial state
- the
Dmatrix contains distance from vertexuto vertexv, where bothuandvare indexes of those vertices in a graph anduis the index of a row andvis the index of the column in any of the matricesRandD - path from
utouis thought to be infinitely long meaning we do not allow this type of paths - in matrix
Rwe define the shortest path fromutovto lie throughv
| D | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | ∞ | 1 | ∞ | |
| 1 | 7 | 0 | 6 | ∞ | |
| 2 | ∞ | ∞ | 0 | 5 | |
| 3 | ∞ | 2 | ∞ | 0 | |
| R | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | 1 | 2 | 3 | |
| 1 | 0 | 1 | 2 | 3 | |
| 2 | 0 | 1 | 2 | 3 | |
| 3 | 0 | 1 | 2 | 3 | |
Step 1
We try to find the vertex which makes the shorter path through itself than the direct path between two vertices. E.g. for every vertex k we find the pair of vertices u and v where path u -> v is longer than the path u -> k -> v. If we found one - we will update the matrices D and R, correspondingly.
For vertex k = 0 we will check each combination of:
paths through 0 starting at 0:
0 -> 0vs0 -> 0 -> 00 -> 1vs0 -> 0 -> 10 -> 2vs0 -> 0 -> 20 -> 3vs0 -> 0 -> 3
paths through 0 starting at 1:
1 -> 0vs1 -> 0 -> 01 -> 1vs1 -> 0 -> 11 -> 2vs1 -> 0 -> 21 -> 3vs1 -> 0 -> 3
paths through 0 starting at 2:
2 -> 0vs2 -> 0 -> 02 -> 1vs2 -> 0 -> 12 -> 2vs2 -> 0 -> 22 -> 3vs2 -> 0 -> 3
paths through 0 starting at 3:
3 -> 0vs3 -> 0 -> 03 -> 1vs3 -> 0 -> 13 -> 2vs3 -> 0 -> 23 -> 3vs3 -> 0 -> 3
As you can see, there are lots of invalid paths here - those which either do not exist or do not make sense. Examples are: paths which do not exist (like 0 -> 3) and paths to any vertex through source vertex (like 0 -> 0 -> 0 and 0 -> 0 -> (any)).
We could easily reduce the amount of the steps performed by the algorithm by throwing few if conditions to check for those cases.
But let's first finish animating this step: there are very few valid paths amongst N * N === 16 of those we've checked. And only one comparison: for path 1 -> 2 vs 1 -> 0 -> 2 we compare 6 (direct) and 7 + 1 = 8 (1 -> 0 and then 0 -> 2).
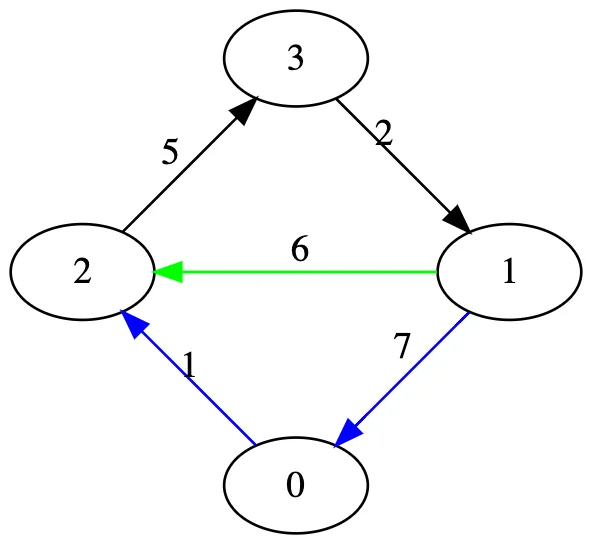
So there are no changes in our matrices.
| D | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | ∞ | 1 | ∞ | |
| 1 | 7 | 0 | 6 | ∞ | |
| 2 | ∞ | ∞ | 0 | 5 | |
| 3 | ∞ | 2 | ∞ | 0 | |
| R | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | 1 | 2 | 3 | |
| 1 | 0 | 1 | 2 | 3 | |
| 2 | 0 | 1 | 2 | 3 | |
| 3 | 0 | 1 | 2 | 3 | |
Step 2
For vertex 1 we will check each combination of:
paths through 1 starting at 0:
0 -> 0vs0 -> 1 -> 00 -> 1vs0 -> 1 -> 10 -> 2vs0 -> 1 -> 20 -> 3vs0 -> 1 -> 3
paths through 1 starting at 1:
1 -> 0vs1 -> 1 -> 01 -> 1vs1 -> 1 -> 11 -> 2vs1 -> 1 -> 21 -> 3vs1 -> 1 -> 3
paths through 1 starting at 2:
2 -> 0vs2 -> 1 -> 02 -> 1vs2 -> 1 -> 12 -> 2vs2 -> 1 -> 22 -> 3vs2 -> 1 -> 3
paths through 1 starting at 3:
3 -> 0vs3 -> 1 -> 03 -> 1vs3 -> 1 -> 13 -> 2vs3 -> 1 -> 23 -> 3vs3 -> 1 -> 3
This case is more interesting - there are more things to compare. Let's see each combination:
3 -> 0does not exist (inf)3 -> 1has length2and1 -> 0has length7, the indirect path3 -> 1 -> 0has length9
Hence we will update matrices D and R reflecting that.
For path 3 -> 1 -> 2:
- there is no path from
3to2directly, so its length isinf 3 -> 1has length2and1 -> 2has length6, the total is8which is infinitely better than infinity
Here are the updated matrices:
| D | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | ∞ | 1 | ∞ | |
| 1 | 7 | 0 | 6 | ∞ | |
| 2 | ∞ | ∞ | 0 | 5 | |
| 3 | 9 | 2 | 8 | 0 | |
| R | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | 1 | 2 | 3 | |
| 1 | 0 | 1 | 2 | 3 | |
| 2 | 0 | 1 | 2 | 3 | |
| 3 | 1 | 1 | 1 | 3 | |
Step 3
For vertex 2 we will check each combination of:
paths through 2 starting at 0:
0 -> 0vs0 -> 2 -> 00 -> 1vs0 -> 2 -> 10 -> 2vs0 -> 2 -> 20 -> 3vs0 -> 2 -> 3
paths through 2 starting at 1:
1 -> 0vs1 -> 2 -> 01 -> 1vs1 -> 2 -> 11 -> 2vs1 -> 2 -> 21 -> 3vs1 -> 2 -> 3
paths through 2 starting at 2:
2 -> 0vs2 -> 2 -> 02 -> 1vs2 -> 2 -> 12 -> 2vs2 -> 2 -> 22 -> 3vs2 -> 2 -> 3
paths through 2 starting at 3:
3 -> 0vs3 -> 2 -> 03 -> 1vs3 -> 2 -> 13 -> 2vs3 -> 2 -> 23 -> 3vs3 -> 2 -> 3
The valid comparisons are:
0 -> 3vs0 -> 2 -> 31 -> 3vs1 -> 2 -> 3
In first case, we compare infinity (0 -> 3) to 1 + 5 == 6 (0 -> 2 and then 2 -> 3).
In second case we compare infinity again (1 -> 3) to 6 + 5 == 11 (1 -> 2 and then 2 -> 3).
In both cases we select the path through vertex 2.
| D | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | ∞ | 1 | 6 | |
| 1 | 7 | 0 | 6 | 11 | |
| 2 | ∞ | ∞ | 0 | 5 | |
| 3 | 9 | 2 | 8 | 0 | |
| R | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | 1 | 2 | 2 | |
| 1 | 0 | 1 | 2 | 2 | |
| 2 | 0 | 1 | 2 | 3 | |
| 3 | 1 | 1 | 1 | 3 | |
Step 4
For vertex 3 we will check each combination of:
paths through 3 starting at 0:
0 -> 0vs0 -> 3 -> 00 -> 1vs0 -> 3 -> 10 -> 2vs0 -> 3 -> 20 -> 3vs0 -> 3 -> 3
paths through 3 starting at 1:
1 -> 0vs1 -> 3 -> 01 -> 1vs1 -> 3 -> 11 -> 2vs1 -> 3 -> 21 -> 3vs1 -> 3 -> 3
paths through 3 starting at 2:
2 -> 0vs2 -> 3 -> 02 -> 1vs2 -> 3 -> 12 -> 2vs2 -> 3 -> 22 -> 3vs2 -> 3 -> 3
paths through 3 starting at 3:
3 -> 0vs3 -> 3 -> 03 -> 1vs3 -> 3 -> 13 -> 2vs3 -> 3 -> 23 -> 3vs3 -> 3 -> 3
This case is the last one. It is similar to the previous two. But please note that we are using the matrix values from the previous step.
For path 0 -> 1:
- direct path from
0to1does not exist, take it asinf - shortest path from
0to3(whichever it is) has length6;3 -> 1has length2; the total path has length8which is better than infinity
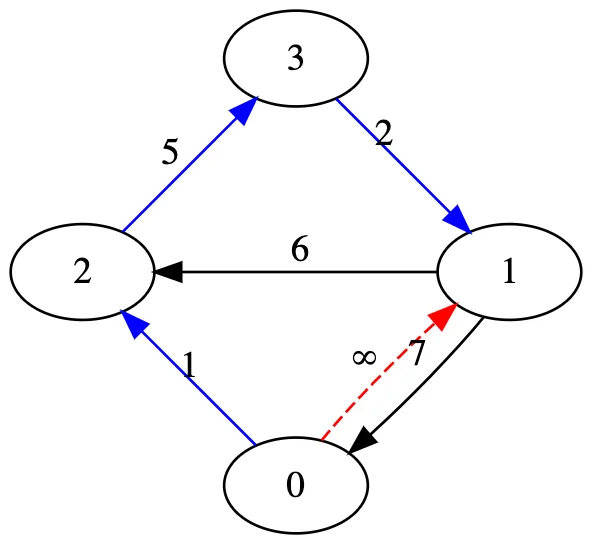
For path 2 -> 0:
- direct path
2 -> 0does not exist - the edge
2 -> 3exists and has length5; path from3to0has length9; so the shortest path from2to0through3will have length9 + 5 == 14
For path 2 -> 1:
- there is no direct path
2 -> 1 - the path
2 -> 3is5and3 -> 1is2, so2 -> 3 -> 1is7
Both matrices R and D will be updated to reflect that:
| D | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | 8 | 1 | 6 | |
| 1 | 7 | 0 | 6 | 11 | |
| 2 | 14 | 7 | 0 | 5 | |
| 3 | 9 | 2 | 8 | 0 | |
| R | |||||
| 0 | 1 | 2 | 3 | ||
| 0 | 0 | 2 | 2 | 2 | |
| 1 | 0 | 1 | 2 | 2 | |
| 2 | 3 | 3 | 2 | 3 | |
| 3 | 1 | 1 | 1 | 3 | |
And then the algorithm is done.
Path reconstruction
In order to reconstruct the path from vertex u to vertex v, you need follow the elements of matrix R, effectively going "through" each vertex:
List<Int32> Path = new List<Int32>();
while (start != end) {
Path.Add(start);
start = R[start, end];
}
Path.Add(end);Let's follow this logic in steps again, "animating" the algorithm. For instance, the longest path in this graph possible, from 0 to 1:
start = 0, end = 1R[0, 1] == 2, start = 2, end = 1R[2, 1] == 3, start = 3, end = 1R[3, 1] == 1, start = 1, end = 1
So the path from 0 to 1 is all the values the start variable takes (except last), namely: 0 -> 2 -> 3.
Summary
The whole code could be wrapped in a couple of methods:
using System;
using System.Collections.Generic;
public class FloydWarshallPathFinder {
private int N;
private int[,] D;
private int[,] R;
public FloydWarshallPathFinder(int NumberOfVertices, int[,] EdgesLengths) {
N = NumberOfVertices;
D = EdgesLengths;
R = null;
}
public int[,] FindAllPaths() {
R = new int[N, N];
for (int i = 0; i < N; i++) {
for (int t = 0; t < N; t++) {
R[i, t] = t;
}
}
for (int k = 0; k < N; k++) {
for (int v = 0; v < N; v++) {
for (int u = 0; u < N; u++) {
if (D[u, k] + D[k, v] < D[u, v]) {
D[u, v] = D[u, k] + D[k, v];
R[u, v] = R[u, k];
}
}
}
}
return R;
}
public List<Int32> FindShortestPath(int start, int end) {
if (R == null) {
FindAllPaths();
}
List<Int32> Path = new List<Int32>();
while (start != end) {
Path.Add(start);
start = R[start, end];
}
Path.Add(end);
return Path;
}
}
public class MainClass {
public static void Main() {
int N = 4;
int[,] D = new int[N, N];
for (int i = 0; i < N; i++) {
for (int t = 0; t < N; t++) {
if (i == t) {
D[i, t] = 0;
} else {
D[i, t] = 9999;
}
}
}
D[0, 2] = 1;
D[1, 0] = 7;
D[1, 2] = 6;
D[2, 3] = 5;
D[3, 1] = 2;
FloydWarshallPathFinder pathFinder = new FloydWarshallPathFinder(N, D);
int start = 0;
int end = 1;
Console.WriteLine("Path: {0}", String.Join(" -> ", pathFinder.FindShortestPath(start, end).ToArray()));
}
}You can read 'bout this algorithm on wikipedia and get some data structures generated automatically here