irrPaint3d

Recently I was reviving some of my old projects. And to my surprise, there were some people actually interested in those! That was a good enough reason for me to revise the old pet projects of mine and exercise my skills (mostly in C++ though).

One really interesting project I had back in the day was irrPaint3d. It all started as an idea for my B.Sc. thesis and the ultimate goal was to enable users paint 3D objects and immediately see the results in realtime, in 3D.

This is a no unique feature nowadays, but back in 2013, to my knowledge, the only way to texture 3D models was to either unwrap them to UV maps and then paint the textures in graphics editor (such as Gimp or Paint.NET) or to use a proprietary software, 3D Coat.

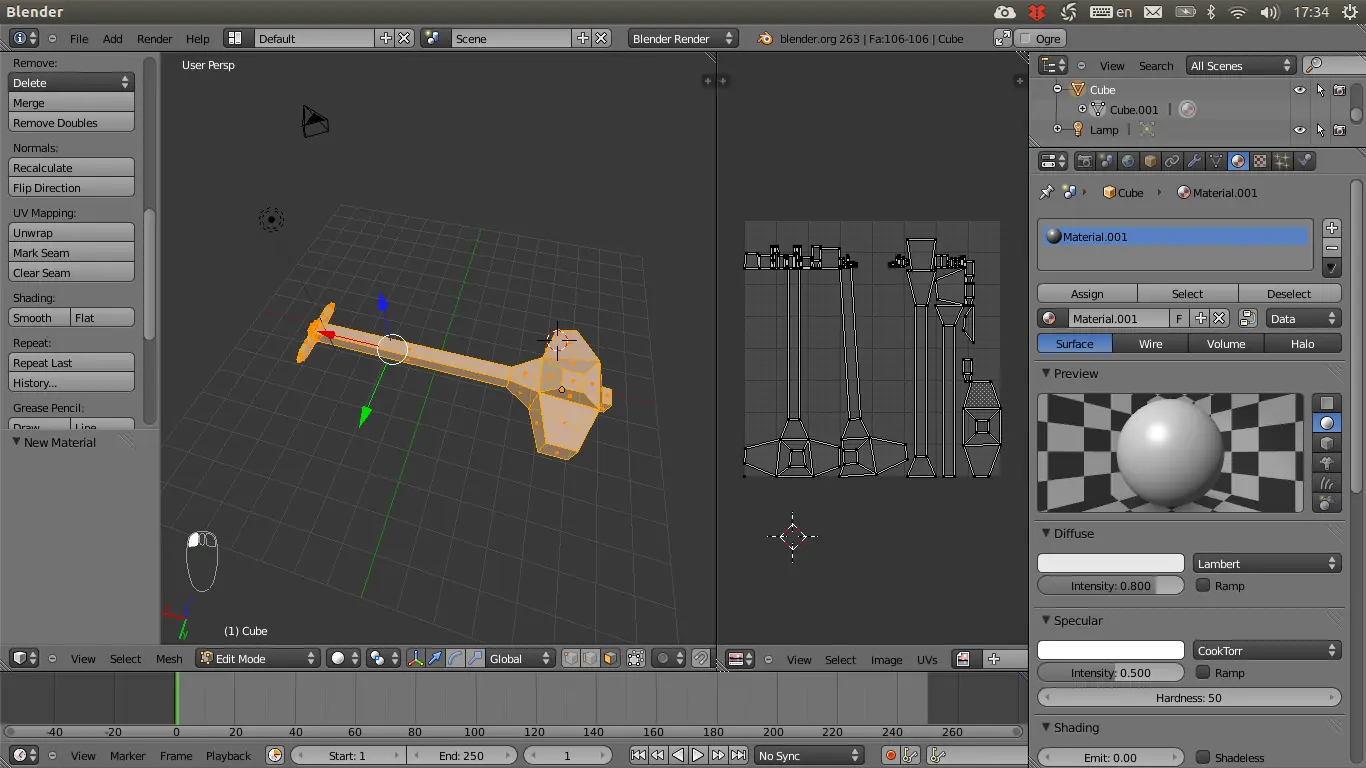
And a mere idea of implementing such tool myself was quite exciting. Darn, if I managed to implement it back in 2013, my thesis would shine among best thesises in my uni!

Long story short, I have failed with that. And now, after spending just few days on this, I am happy to say I have achieved something with yet another glorious pet project revival:

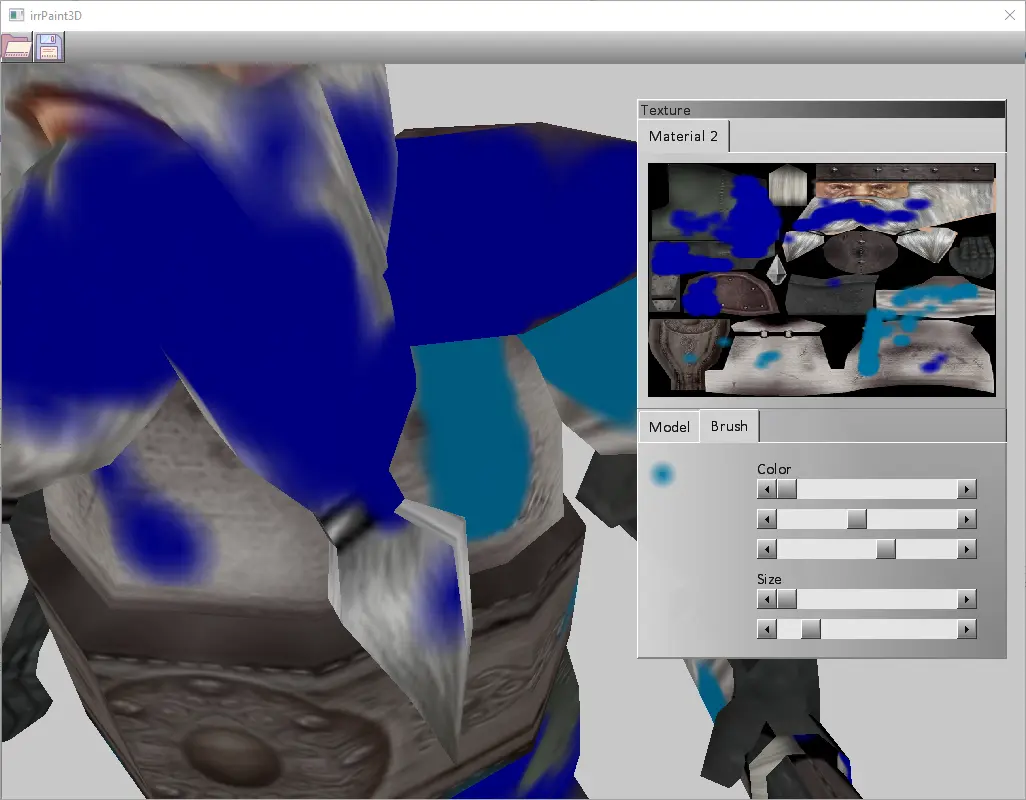
And it actually allows to paint the model in 3D, displaying the results in real-time!

A bit of history on how I got there and maths behind the solution under the cut.

A brief history

Back in the day I have put too little thought into the project so I ended up trying to implement LSCM algorithm to unwrap 3D models. And after numerous failures I came up with my own, very simple algorithm to unwrap models and that made my B.Sc. thesis.

The algorithm was a simple system of numerous circle equations following the logic of pinning down a vertex from a triangle on 2D plane at point (0, 0) and figuring out the 2D coordinates of the other two vertices using the lengths of the triangle edges in 3D, using two circles, with centres at the pinned point ((0, 0)) and radiuses equal to triangle edges’ lengths. The circles would overlap in two points, and both are candidates for the other two triangle’ verices mapping:

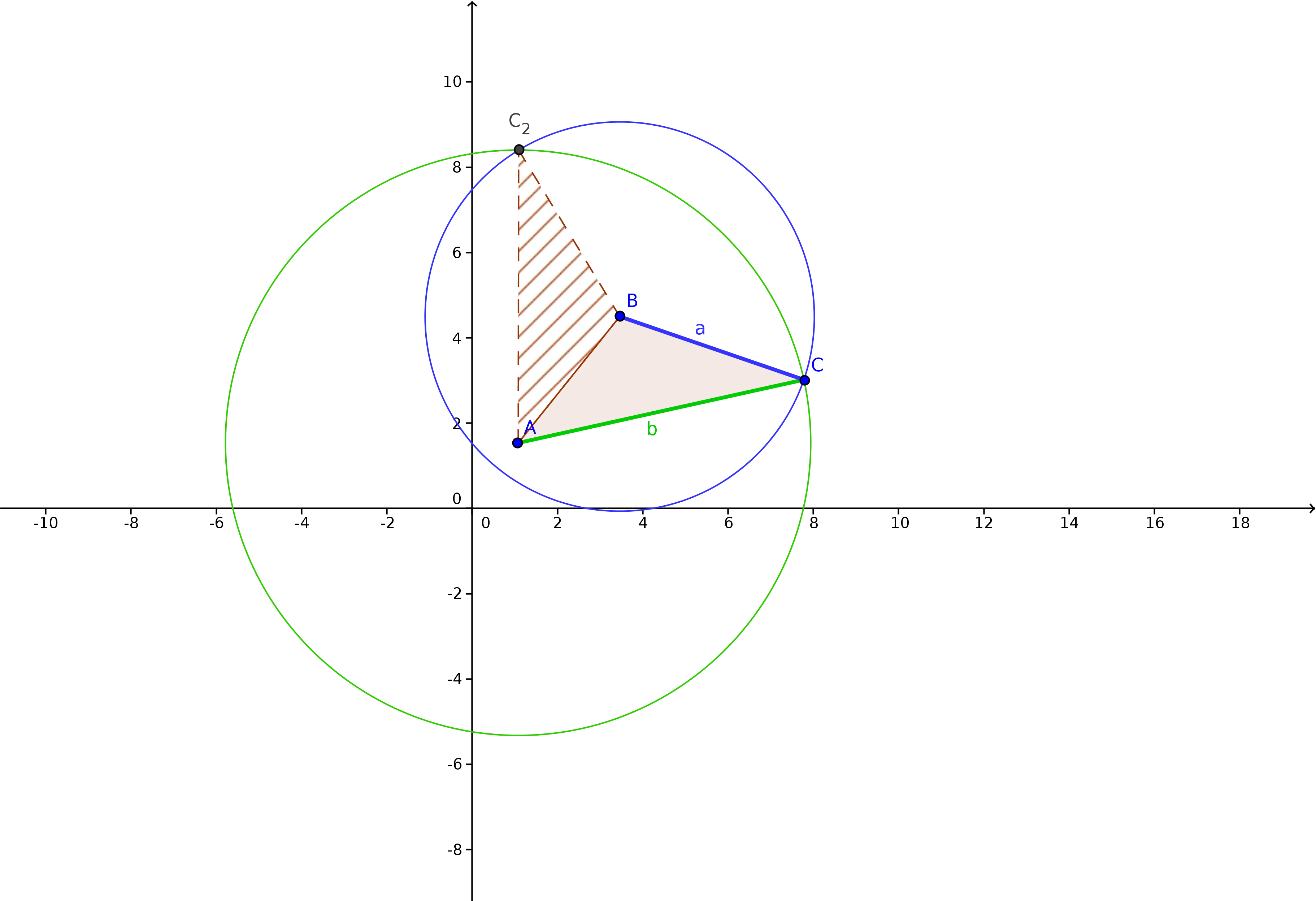
The algorithm… worked… in some cases:

I did try to understand the concept of barycentric coordinates, but that is something completely different to what I imagined, apparently:

The maths behind

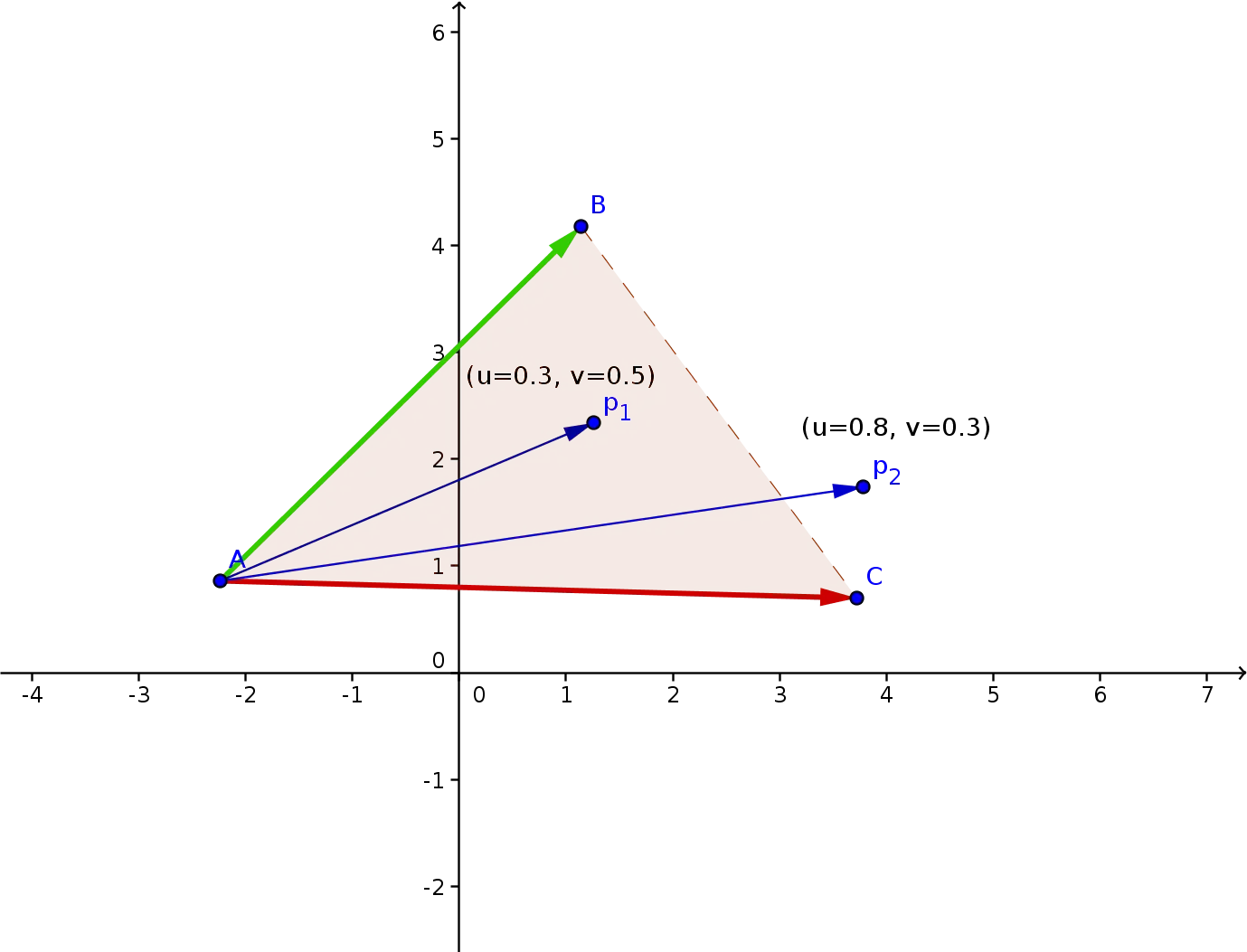
With my new approach, I took an idea from the enormously cool introduction to computer graphics and the math underneath by One Lone Coder. The idea itself is rather trivial: any vector could be represented as a sum of two other (not necessarily orthogonal) vectors (plus a condition that the angle between the two should not be 180 degrees).

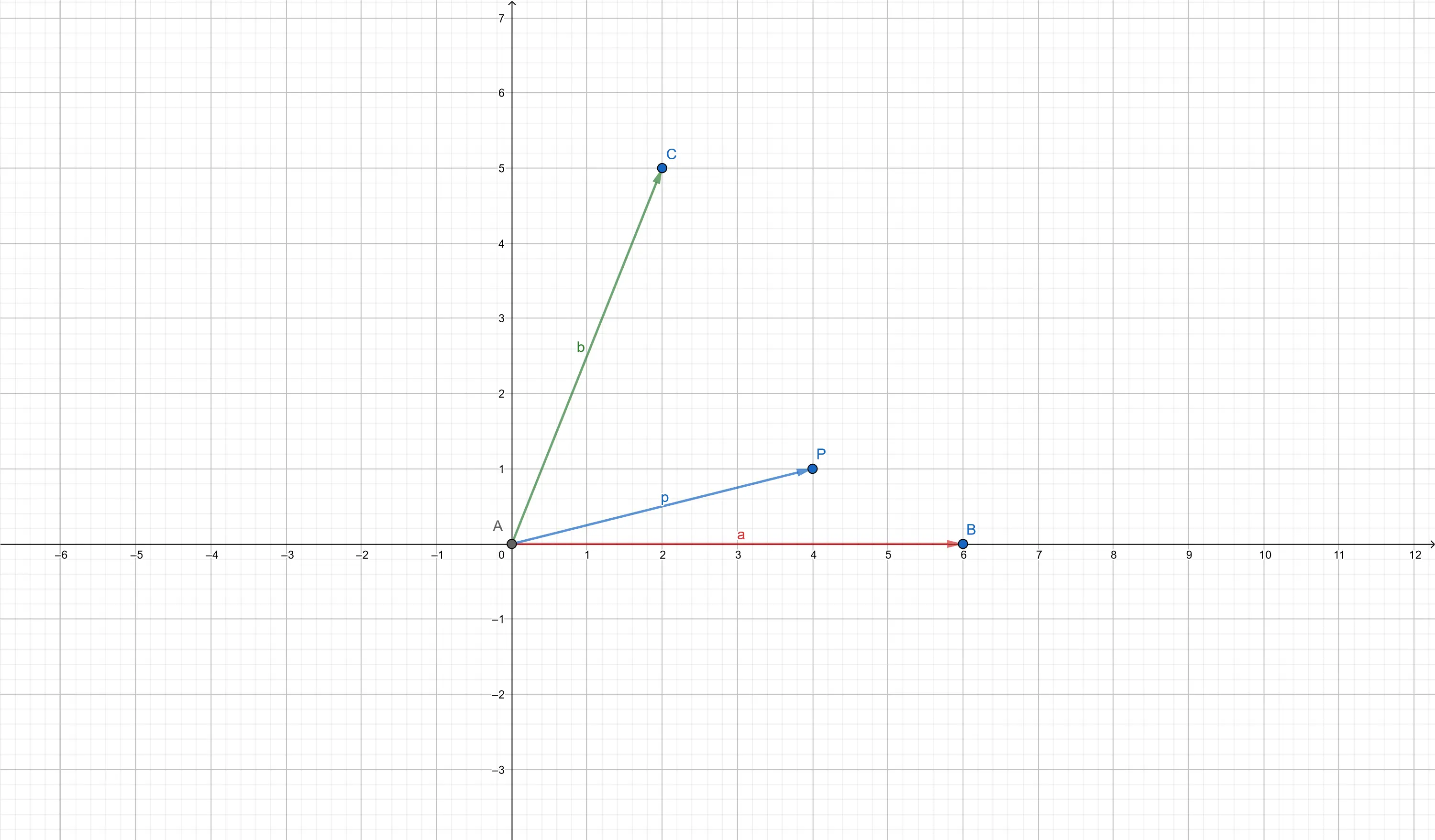
In the example above, vector p could be represented as a sum of vectors a and b, each multiplied by certain coefficients: p = u*a + v*b.

And the dimensions of the vectors do not matter - this logic will work just as well in 3D as in 2D.

Now, if we have a triangle in 3D, ABC and a point inside that triangle P, we can represent the vector AP as a sum of vectors AB and AC multiplied by some coefficients, u*AB + v*AC = AP.

It is only the matter of finding those coefficients, u and v. Luckily, this could be done with a system of three linear equations with just two variables:

ax * u + bx * v = px
ay * u + by * v = py
az * u + bz * v = pz

where

• vector AB <=> a(ax, ay, az)
• vector AC <=> b(bx, by, bz)
• vector AP <=> p(px, py, pz)

Simply using the substitution, we can first express u as a function of v and then calculate v to then find u. The only bit here is that the multiplier of v must not be zero.

In C++ this looks like this (I am using Irrlicht for this application, so bare with irr:: namespaces):

irr::video::S3DVertex A, B, C;

// find A, B and C from the selected triangle
// also collisionPoint is the point in question, inside the selected triangle

irr::core::vector3df a = B.Pos - A.Pos;
irr::core::vector3df b = C.Pos - A.Pos;
irr::core::vector3df p = collisionPoint - A.Pos;

float u, v;

// au + bv = p
if (a.X != 0) {
    v = ((a.X * p.Y) - (a.Y * p.X)) / ((a.X * b.Y) - (a.Y * b.X));
    u = (p.X - (b.X * v)) / a.X;
}
else if (a.Y != 0) {
    v = ((a.Y * p.Z) - (a.Z * p.Y)) / ((a.Y * b.Z) - (a.Z * b.Y));
    u = (p.Y - (b.Y * v)) / a.Y;
}
else if (a.Z != 0) {
    v = ((a.Z * p.X) - (a.X * p.Z)) / ((a.Z * b.X) - (a.X * b.Z));
    u = (p.Z - (b.Z * v)) / a.Z;
}
else {
    throw "Invalid input - zero basis vector";
}

Now the last bit of the maths: given the points of a selected triangle all have their texture coordinates (hence using irr::video::S3DVertex), how do we find the texture coordinates of a given point P? Simple: by applying the same vector maths to the texture coordinates: we can represent a given triangle in 2D space of texture coordinates and using the vectors AB, AC and AP and the multipliers u and v which we have just obtained from 3D space, we can “interpolate” the texture coordinates of vector AP:

irr::core::vector2df t2 = B.TCoords - A.TCoords;
irr::core::vector2df t1 = C.TCoords - A.TCoords;

irr::core::vector2df uvCoords = A.TCoords + t1 * u + t2 * v;

The rest is just rendering and drawing on a texture. The full version of the project is available on GitHub.